第一章 绪论
1.1 研究目的及意义
随着我国交通事业的迅速发展,连续钢箱梁桥应用越来越广泛[1],钢箱梁能够实现混凝土桥梁所不具备的特点,同等梁截面刚度的情况下[2],钢箱梁自重会远远比混凝土梁小,因而使得连续钢箱梁桥有更大承载力,且主梁变形会更小[3],行车更舒适。连续钢箱梁桥是最典型薄壁结构,满足往轻质高强桥梁发展的方向,不仅在经济、使用性能上优于其他桥型,而且还能够提高空间利用效率,符合城市绿色要求[4]。为保持截面的工作性能并提高连续钢箱梁的承载能力,钢箱梁需要布置一定数量的加劲肋构件。因而使得钢箱梁桥细部构造多且对分析应该考虑细部部分影响因素,连续钢箱梁桥抗弯承载力较大[5]。首先是因为主梁各部位均可承受比较大的正负弯矩。再次是因为截面荷载横向分配较均匀,适合于扭矩较大的曲线桥梁。连续钢箱梁桥具有较强的横向承载力[6]。钢箱梁横向刚度及横向整体性较强,较小的梁高及横向加劲作用使主梁可以抵抗很大的水平作用力。钢箱梁因闭口薄壁结构受力后会产生纵向弯曲、扭转变形、畸变及横向挠曲四种基本变形并且产生相应应力[7]。连续钢箱梁稳定问题是影响其运营安全的重要因素[8],钢箱梁桥高强轻质的特点使得稳定性问题显得更加重要。为了提高箱梁承载能力需在顶底板纵向设置一定加劲肋,但是如果加劲肋数量过多将会增加梁体自重,并造成材料的浪费,材料性能得不到充分地发挥。加劲肋的可分为开口、闭口两种形式截面。开口式加劲肋主要可分为 L 形和倒 T 形,平钢板形;闭口式加劲肋的主要分为梯形三角形 V 形 U形。闭口加劲能够提供较大抗扭刚度、抗弯刚度进而改善钢桥受力状态,加劲间距对连续钢箱梁稳定性也及其重要。考虑了几何非线性情况下学者们做了大量工作,但是如果想要更加深入的了解到稳定问题复杂的实质,必须同时分析材料非线性本构关系以及几何非线性关系,本文重点研究了双重非线性下加劲肋对连续钢箱梁的稳定性影响[9]。
........
1.2 钢箱梁稳定性研究现状及发展方向
国外研究现状非线性系统稳定性的分析理论主要由三大理论支撑,即李亚普诺夫稳定性理论、输入输出稳定性理论及绝对稳定性理论[10]。1892 年,李亚普诺夫院士在他的博士论文里提出李亚普诺夫稳定性理论,目前仍然被广泛使用,但它只可以用来判断系统稳定性的充分条件[11],并没有形成李亚普诺夫函数的通用办法。基本思想是将泛函分析方法应用于普通动态系统分析中去,分析方法比较简便,确能得到比较笼统的稳定性概念。前苏联学者鲁里叶、波斯特尼考夫所提出绝对稳定性概念,影响最为广泛的是波波夫判据及圆判据。但在变量较多的非线性系统中也很难得到推广。1744 年欧拉曾研究了压杆变形并进行研究计算弹性压杆屈曲理论。在此基础上提出欧拉公式[12]。彭加瑞明确阑述了稳定概念且推广到了流体力学层流稳定问题。而后恩格塞提出切线模量 E 来代替欧拉公式中的弹性模量概念并且认为临界荷载作用情况下柱子开始弯曲的时候,它的凹侧应力随着切线模量增加而增大,而凸侧应力则会随着弹性模量增加而卸载,因而认为有效模量是切线模量与弹性模量的函数[13]。布里安随后提出简支矩形板单向均匀受压的稳定分析,普里特尔、米歇尔几乎同时发表关于梁侧倾问题研究成果,在此之后结合各种形式的荷载与支承情况及构造的桥梁结构稳定性理论而得到的不断发展[14]。在实际工程中,连续钢箱梁在施工阶段很可能存在几何非线性和材料非线性问题,在杆系结构的几何非线性分析中,研究者们研究的主要是梁柱理论或者它的改进形式,大多根据梁理论[15]。D.L.Karabalis 与 D.E.Beskos 分析研究弹性阶梯形梁柱的几何非线性效应,并考虑到大位移所导致的几何非线性的行为,而采取修正构件的几何形状,也就是用拖动坐标法来不断进行修正节点的坐标,以至于最终能够找到这个变形之后的平衡位置和它所对应内力[16],此种方法能够跟踪构件实际的变形位置,构件在承受超载作用过程中,部分构件的应力超过材料本身的弹性极限的超限现象,虽然该种现象具有局域性,但构件的损伤与破坏基本都是由这些区域向外延伸的,从而导致了结构的失效[17]。Timoshenk 梁理论则放弃平截面的假定,轴向和剪切及弯曲效应则采用平动转角位移插值法进行计算,并提出大位移及小应变和大转动平面,Timoshenko 的梁单元体是新的几何刚度矩阵[18]。Namini 曾做过一系列的研究,研究内容表明了,考虑构件的几何非线性与材料非线性受力特征后,钢箱梁桥、稳定安全系数能够得到一定的降低,从而稳定问题己经转化成为结构极限承载力的问题。Scanlan 的模型实验研究[19],把小曲率钢箱梁作为工程背景,并采取有限元非线性模型与实验相结合来分析横隔板对钢板应力的影响。
..........
第二章 非线性稳定分析理论和方法
2.1 概述
19 世纪末期,相关研究者就了解到固体力学线性理论在很多时候并不适用,所以开展研究了固体非线性力学;到 20 世纪中期,非线性力学的相关研究结果为后续研究打下了一定的理论基础;但最大的问题是计算较为复杂,想要用解析法解决非线性力学的问题相当困难。20 世纪 60 年代末,非线性力学的相关问题才得以解决,这主要基于有限元与计算机的结合[32]。相关研究表明[33]:固体力学主要有三个基本方程,分别是几何运动方程、本构方程和平衡方程。而固体力学的经典线性理论主要是基于三个基本的假定:约束假定为理想的约束、位移微小、材料应力应变均满足胡克定律[34],就是这三个假定使得三组基本的几何方程成为线性的,但如果所要研究的对象不能同时满足这三个基本假定[35],就会出现各种非线性的问题,倘若继续按照线性方法去解决问题,那将失去研究意义[36]。常见的非线性问题主要有几何非线性问题、接触问题及材料非线性问题[37],非线性问题主要是因为所使用的材料不能满足胡克定律,由材料的应力应变的非线性关系所引起的[38]。其中,几何非线性问题的出现主要是因为不考虑小位移的假设,严格分析单元体的几何尺寸及形态的变化,进而获得非线性的几何运动方程,致使控制方程的非线性问题频繁出现。单元体非线性的平衡方程主要建立在结构变形的位置,受载后的应力、位移状态、变形及材料等因素决定了单元体的刚度。接触问题主要因为研究对象不满足理想约束这一假定而引起的,呈现为边界约束方程的非线性问题[39],同时,单元体受力后其边界条件是未知的。研究表明[40],所谓的平衡方程的建立都是在单元体受力变形的位置上才可以满足,也只有这时候的平衡才具有研究的意义[41]。倘若单元体的受力状态因受力变形而发生较为显著的变化,必须使用非线性方程进行分析才可以解决问题。若桥梁的部分结构正在承受超载作用[42],其构件的盈利将会超过材料本身的弹性极限,导致桥梁部分构件损坏无法修复,最终使得构件失去原本的作用;这里,当桥梁构件承受的应力超过弹性极限的时候,材料的弹性模量与其应力构成函数方程,非线性问题将会出现[43]。因此,研究结构非线性条件的问题,对于构件极限承载力的分析及桥梁非线性问题的解决具有比较实际的意义[44]。
........
2.2 非线性有限元理论
单元体几何非线性理论大致可以分为有限位移理论(即大位移小应变)和有限应变理论(即大位移大应变)两种。而对于桥梁施工中的非线性问题往往都是有限的位移问题,桥梁构件的几何非线性平衡方程,一般都是将桥梁结构看做杆系结构,以其有限位移理论为基础进行建立,平衡方程建立过程中,需要考虑三个几何非线性的效应:杆单元模拟索类构件时由索垂度引起的单元刚度的变化、大位移对构件平衡方程建立的影响以及单元初内力对单元刚度矩阵的影响[45]。分析连续钢箱梁结构的静力非线性时,只需要考虑后两种的几何非线性效应,大位移对结构平衡方程的影响要用 UL 列式进行分析,且单元初内力对单元刚度影响的研究要用几何非线性的刚度矩阵进行计算。
............
第三章 连续钢箱梁有限元分析............14
3.1 线性稳定分析.............14
3.2 非线性稳定分析.........15
3.3 有限元模型的建立.....16
3.4 本章小结.........21
第四章 加劲肋对钢箱梁线性稳定的影响分析............22
4.1 不同参数对钢箱梁线性稳定的有限元分析.............22
4.2 结果分析........41
4.3 本章小节.........42
第五章 加劲肋对连续钢箱梁非线性稳定的影响........44
5.1 第二类稳定理论.........44#p#分页标题#e#
5.2 不同参数的连续钢箱梁的荷载-位移曲线...............45
5.2.1 不同加劲肋形式和间距的荷载—位移曲线...............45
5.2.2 不同加劲肋厚度的荷载—位移曲线...............47
5.3 结果分析.........49
5.4 加劲肋的合理选取.....49
5.5 本章小结.........57
第五章 加劲肋对连续钢箱梁非线性稳定的影响
为了解加劲肋对连续钢箱梁非线性稳定的影响,本章运用桥梁通用有限元软件 ABAQUS 对连续钢箱梁建立壳单元模型,同时考虑材料非线性、几何非线性和初始几何缺陷的影响,分析不同加劲肋形式、加劲肋间距和加劲肋厚度对连续钢箱梁的非线性稳定性影响,得到不同参数下的连续钢箱梁的极限承载力,定性分析了加劲肋对连续钢箱梁的非线性稳定的影响。
5.1 第二类稳定理论
连续钢箱梁桥的第二类稳定问题是指结构随着荷载的不断增加在最不利位置首先出现塑性变形,当荷载达到一定数值时,即使不再增加,结构变形也会迅速增大至使结构破坏。这个荷载值实质上是连续钢箱的极限荷载,也称临界极限荷载,因此第二类稳定也称极值点失稳[63]。第二类稳定问题的实质即结构的稳定极限承载力分析。桥梁结构的失稳伴随结构的大变形并且是逐步加载的过程。第二类稳定问题其实是非线性极值问题,即极限承载力问题,极限承载力分析中,需要考虑到几何非线性和材料非线性,结构失稳常常为大位移、大应变,一般须考虑双重非线性,材料非线性通过模型建立时使用的强化弹-塑性本构关系引入,几何非线性通过引入初始缺陷考虑,将有限元单元线性屈曲计算得到失稳模态作为初始缺陷施加到钢箱梁模型上,初始缺陷可以按 2%来考虑[64]。
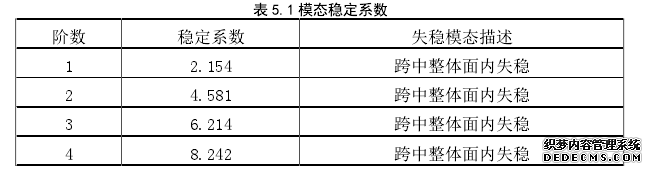

.......
结论
本文利用有限元软件 ABAQUS 对连续钢箱梁的非线性稳定进行了探讨,以工程实例为研究对象,重点分析了不同加劲肋形式、加劲肋间距和加劲肋厚度对连续钢箱梁非线性稳定的影响,通过研究顶底板加劲肋对连续钢箱梁非线性稳定的影响,得到如下结论:(1)不同加劲肋间距对连续钢箱梁的稳定性影响差异较大,在一定范围内,连续钢箱梁的非线性稳定性随着加劲肋间距的减小而增大,加劲肋间距过小对连续钢箱梁的非线性稳定性影响不大,由于加劲肋密度越大,钢箱梁的抗扭刚度越大,抗弯刚度的影响并不明显,但是达到一定范围,增加加劲肋的数量对钢箱梁抗扭刚度影响并不明显。(2)通过改变加劲肋形式进行连续钢箱梁非线性稳定分析,U 形加劲肋比T 形加劲肋更能提高连续钢箱梁的非线性稳定性,增大纵向加劲肋会减弱连续钢箱梁因弯曲引起的应力,横向加劲肋能够分担剪切引起的应力,T 形加劲肋更能提高连续钢箱梁的抗弯性能和抗扭性能,在同等条件下,U 形加劲肋比 T 形形加劲肋更能提高连续钢箱梁的非线性稳定性。(3)通过改变加劲肋厚度进行连续钢箱梁非线性稳定分析,加劲肋厚度越大,连续钢箱梁线性稳定性加强,但是厚度的增加并不能使连续钢箱梁线性稳定显著增加,变化幅度非常小,因为厚度的增加对构件抗弯、抗扭性能的提高并不明显,一般不用增大加劲肋厚度来提高钢箱梁的非线性稳定性。(4)非线性稳定分析比线性稳定分析更符合实际,由于线性稳定分析没有考虑大变形的影响,而材料性能的模拟仅使用了材料的弹性模量,并未进行材料的屈服与破坏应力的判别,所有计算出的临界荷载普遍较高,非线性稳定考虑了大变形、材料非线性,、几何非线性和初始缺陷等问题,连续钢箱梁的非线性稳定性分析结果远小于线性稳定,并且随着加劲肋的不同,非线性影响程度将也逐渐加剧,非线性稳定分析比线性稳定分析的结果更为符合实际。(5)连续钢箱梁的最大设计剪力随着加劲肋厚度的增加而增加,当厚度达到一定范围,加劲肋厚度对钢箱梁最大设计剪力影响不大,这是由于纵向加劲肋主要对抗剪性能起作用,加劲肋厚度的增加使钢箱梁的抗扭刚度增大。(6)在同等条件下,因为 U 形加劲肋比 T 形加劲肋的抗弯刚度大,U 形加劲肋比 T 形加劲肋情况下的钢箱梁最大设计弯矩大。
..........
参考文献(略)

