第一章 绪论
关于生物演化的独立思想在18世纪甚至更早就已经诞生了,这些演化论的观念是建立在变异和自然选择的基础上的,这是由伟大的自然科学家Charls Darwin通过大量的观察得到的[1]。几乎在同一时间,Greogor Mendel揭示了遗传规律,他是通过展示精心设计的植物的培养试验和统计结果来揭示遗传规律的。达尔文的《物种起源》是最早的关于物种演化的理论[1]。整个理论用纯文字来阐述,虽然没有一个公式,但却把达尔文想要表达的自然选择理论描述得很清楚。但是我们知道,没有定量就不能预言,也不能应用到实际,因此,我们有必要把达尔文的理论定量化,这就引起了后来学者对生物演化的各种定量的模型的探讨。这些模型的研究可以追溯到1931年Wright[2]写的《Evolution in Mendelian populations》和1958年Fisher [3] 写的《The Genetical Theory of Natural Selection》,他们的模型都是在分子水平上考虑突变和选择。突变始终是遗传变异的最终来源,而选择则是把优势表型保留下来,把劣势表型消除。但他们的模型中通常考虑的是每个位点有两个等位基因[2,3]。直到上个世纪五十年代末,没有突变,只有选择的多等位基因模型的结果才得到证实。随后,在20世纪六七十年代,出现了比较有影响力的两个生物演化动力学模型Eigen模型[4,5,6,7]和Crow-kimura模型[8,9,10]。 Eigen模型即准物种模型是伴随着分子遗传学诞生的,出现在生物学中。它是在突变和选择的条件下物种结合的一个系综,是首先由Eigen为描述RNA分子易出错复制的理论描述提出的,是分子演化理论的一个重要分支[4]。
Crow-kimura模型是由Crow和Kimura提出无限等位基因模型,他们是在群体是无性生殖的体系假定下,考虑每个等位基因可以突变到相邻的两个等位基因上,这一模型曾得到广泛的研究。 Eigen模型和Crow-kimura模型都对生物演化的分子动力学描述做出了很大的贡献。但是这些模型都是对演化的确定性描述,把模型随机化还比较少。因此,我们现在的研究大都趋向于在这两个模型的基础上做出更精确,更真实的随机模型,从而推动演化动力学理论的进一步发展。本项研究主要以 Eigen 模型为理论框架,把基因序列中某一位点的突变率是看成一个随机的高斯分布量。因为我们知道演化在分子水平是受多方面因素影响的,无论是基因因素还是基因外环境因素,突变率都应该是随空间和时间改变的,所以,把它高斯随机化处理是对 Eigen 模型趋近现实的进一步改进。同时,我们在突变率随机化模型的基础上对适应值做了定量改变和随机化处理,看适应值与突变率的关系,及这两个变量同时随机化对物种演化的不同影响。总之,在物种演化中考虑随机因素是对演化模型的进一步补充,也是现在演化理论研究的热点。
………….
第二章 物种演化的基本理论及主要模型
2.1 达尔文体系
进化是生物学灵魂,没有进化就没有生物[11]。物种演化的三个基石分别是复制(Replication)、选择(Selection)和突变(Mutation)。它们三个的含义各不相同,但有联系。复制也可看作再生,它保证生命一代又一代地可以延续下去,其中包括基因物质以DNA或RNA的形式复制,细胞再生等等,在各个层次上都可以发生。选择发生在两个以上不同个体,种群等之间的竞争,优胜弱汰。突变产生生物的多样性为在竞争过程中出现生物进化创造了必要条件。在分子水平,DNA或RNA 在复制过程中发生的差错称为突变,这种突变会导致奇妙的进化,所以说,生物生命在犯错误中得到益处。首先,考虑仅有两个不同类型的情况,分别用A和B表示。设 1 u 代表从A到B的突变率, 2 u 表示从B到A的突变率,并设A的频率为x,B的频率为y,且它们的复制率,再生率,或适应度(fitness)均为1(量纲为时间的倒数)。即,只单纯考虑突变情况。
………..
2.2 基本概念
在了解Eigen模型之前,首先要理解几个概念:适应度,适应面和序空间(Fitness , fitness landscapes and Sequence Space)。序列空间是用汉明距离(Hamming distance)来构成的[6]。在这个空间中每一点表示一个基因序列,点和点之间的距离用汉明距离来表示,所有这些点的空间结合就组成了序列空间。进化过程可以被描述为在序列空间的一条轨迹[6]。适应面(Fitness landscapes)[4]适应面这个概念首先是由Sewell Wright 于20世纪30年代提出来的,20世纪70年代,Manfred Eigen与Peter Schuster把适应度与序列空间相结合,令每个序列有特定的适应度(用一个点表示),我们就可以在L(基因序列长度)维序列空间中构造出一个适应度山脉(相当于位能曲线,位能面),这些点的集合所组成的面就叫作适应面。准物种[4]准物种是指在突变和选择过程中产生的相似基因序列的一个系综,这概念由化学中的“物种”借用过来的。在无突变的情况下,每一个种群只有一种表现型(野生型),即只有一个物种。当有突变的时候,种群不变,但种群下的物种多了。定义原来的物种的基因序列为主序列,当突变不太大时,主序列的相对丰度(浓度)比较大,而其它突变序列的相对丰度比较小,所以,其它突变物种的分布会表现出向原来拥有主序列的物种上靠拢,这些物种统称为准物种。
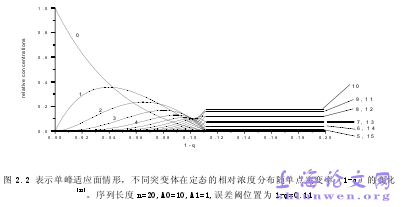
…………
第三章 突变率随机化的误差模型....15
3.1 确定性模型的验证.........15
3.2 突变率高斯随机化的验证.......17
3.3 随机化的突变率对 Eigen 模型的影响.........17
3.4 误差在随机模型中的变化.......19
3.5 突变率随机化模型的数据统计....21
3.6 小结......22
第四章 定量改变适应度对突变率随机化模型的影响....23
4.1 适应度定量改变原因.....23
4.2 主序列与突变序列的适应度的比值为一个数量级下的结果....23
4.3 主序列与突变序列的适应度的比值为两个数量级下的结果....24
4.4 主序列和突变序列的适应度的比值为三个数量级下的结果....26
4.5 小结......28
第五章 适应度和突变率单独随机化对物种演化的不同影响........29
第六章 适应度和突变率同时随机化模型
6.1 适应度和突变率同时随机化模型
适应度和突变率同时随机化模型是对原来适应度随机化模型和突变率随机化模型的进一步补充。在这个模型中,两个变量同时作高斯随机化处理。其中,适应度看成是单峰的,而且,主序列和每一种类型突变体的复制速率都看成是随机的,我们将描述物种演化的确定性Eigen模型改造成了一个随机模型,使得Eigen模型能够更真实地描写物种的演化过程。在突变率和适应度同时随机化模型中,我们发现它与之前的适应度单独随机化和突变率单独随机化模型近似满足线性叠加的关系。并且这种两个变量同时随机化模型与原来的变量单独随机化模型有相同的规律。即,对同一个基因序列,突变率的涨落强度趋近于零时,误差阈仍是是一个相变点,这说明误差阈对小的扰动是稳定的;当突变率和适应度的涨落强度逐渐增大时,误差阈由一个相变点变为一个有一定宽度的转变区域。这是个很重要的现象,它对于解决实际问题有意义。比如在研究抗病毒案例时,原来的确定性模型所使用的剂量是使其突变率达到误差阈即可。但考虑突变率的随机性后,使用的剂量应使病毒突变率达到转变区域的上限才能把它完全消灭掉。通过调研发现,已经有实验通过利用诱变剂或者改变环境的方法来控制复制的精度,从而驱使病毒群体越过误差阈而被灭绝。这和我们理论增加突变率的涨落强度来模拟准物种的演化行为相一致[32,34,35]。
……….
结论
在物种演化模型中,最有代表性的是Eigen模型,它是建立在单峰适应面上的确定性模型。大量研究表明,准物种分布会随着突变率的增加出现一个误差阈[4]。这一相变使准物种从适应面的高峰突然趋向消亡。然而,这一结论是在确定性模型下得到的。众所周知,物种演化在分子水平上是受多方面复杂因素影响的,无论是基因因素还是基因外的环境因素,都能导致突变率和适应度随空间和时间的不规则改变。因此,在本项工作中,我们以 Eigen 模型为基础,把突变率处理成高斯随机变量,从而使 Eigen 模型转化成突变率高斯随机化模型,并对这种模型进一步延伸,把适应度做定量改变和高斯随机化,进而观察适应度对突变率随机模型的影响及突变率和适应度同时高斯随机化模型的特点。并把这些模型与之前的适应度高斯随机化模型[12,28,29]和确定性模型[4,5,8,9]进行了对比。从这些随机模型与确定性模型的比较中,我们发现随机模型中的误差阈不再是一个尖锐的相变点,而是一个随着变量的涨落强度的增大而逐渐变宽的相变区域。而且对突变率随机模型中的适应度做定量改变时,我们发现定性来看,误差阈随适应度中主序列和突变序列的比值的增大而增大;定量来看,准物种的分布只与序列间适应度的比值有关系,与各序列适应度的大小无关。若对适应度和突变率分别作随机化处理,我们发现在同样参数下,适应度随机化时对误差阈的影响比较小,而突变率随机化时对误差阈的影响比较大。这说明突变率随机化对物种演化作用更明显。如果突变率和适应度同时随机化,我们发现其它参数相同的时候,它与之前的适应度单独随机化和突变率单独随机化模型得到的误差阈的宽度近似满足线性叠加的关系。#p#分页标题#e#
…………
参考文献(略)

