本文是一篇硕士论文,硕士论文应当具有一定的理论深度和更高的学术水平,更加强调作者思想观点的独创性,以及研究成果应具备更强的实用价值和更高的科学价值。(以上内容来自百度百科)今天为大家推荐一篇硕士论文,供大家参考。
第 1 章 绪 论
1.1 研究意义
航空发动机、汽轮机、压缩机、风机、水泵等旋转机械在国防、能源、电力交通、机械等领域中应用广泛并发挥着重要的作用。转子系统作为旋转机械系统的核心组成成分,以其动力学性能不断支配着工作性能及安全质量。各种形式的故障的发生都可能会使转子系统无法正常的工作,有时可以造成重大的人员伤亡以及经济损失。以涡轮发动机为代表的复杂的旋转机械,引起其振动的因素有很多。当其振动十分剧烈时就会引发机器损坏、人员伤亡的重大事故。因此,研究带转子系统的动力学问题,揭示引发转子系统故障的因素,建立合理的可靠性分析模型,了解设计参数对转子系统可靠性的影响程度是十分重要的。早期的转子系统转速较低,引起其振动的主要原因为圆盘的偏心,即圆盘重心与转轴轴线不重合。采用静平衡的办法减小其偏心距就可以基本消除转子系统的振动。随着科学技术与现代化工业水平的发展,转子的转速得到了提升,圆盘也不再是之前的简单的片状,而是朝着更复杂的圆柱状或圆锥状发展。这时用静平衡方法已经不能消除转子的振动,而要考虑转轴的弯曲振动与圆盘质量和偏心距大小的关系,采用动平衡以消除振动。当转子的转速上升到某个特定的转速时,虽然经过了动平衡,但转子系统还是会发生剧烈振动。此时转子的转速为临界转速。临界转速与固有频率是高速转子系统的重要动力学特性参数,它们决定着转子系统的可靠程度。影响转子系统临界转速与固有频率的因素包括转子系统的结构参数与力学参数。这些参数有些对转子系统的可靠度是比较敏感的,而有些是不敏感的。因此,作为优化设计的奠基,分析转子系统的可靠性灵敏度尤为重要[1]。
.........
1.2 结构可靠性设计的发展历史和现状
结构体系的分析和设计方法始终与科学技术的发展有着紧密的关系。传统的结构设计与分析采用的是确定性的方法,即在设计与分析中涉及到的参数均为确定值。事实上,在实际的工程问题上,由于零件经过生产加工以及装配等过程方产生误差,使得这些参数不再是某一确定的值,而是具有一定分布规律的随机变量。采用确定性方法对结构分析与设计显然不再合理,而应对结构进行具有随机性的可靠性分析。结构可靠性对保障结构的安全是至关重要的,其最初是以电子元器件可靠性为基础而发展起来。相对于电子元器件的可靠性,结构可靠性的发展较为落后,主要表现在两方面:其一是由于结构的非标准化程度较高,使得结构可靠性分析所需的数据较为匮乏;其二是由于复杂的结构的可靠性分析涉及到动力学与运动学等理论,而这些理论的不完善也在很大的程度上制约结构可靠性发展。机械可靠性基本理论的研究大约可以追溯到 20 世纪 20 年代。1926-1929 年前苏联的 H. A. XauHOJioB 和 M. MaftepoB 制定了概率设计的方法,但由于该年代从事结构可靠性理论研发的学者较少,理论还未足够成熟,因此未应用到实际工程中[2]。随着机械制造水平的不断进步,直至 20 世纪 30 年代,主要应用可靠性理论对飞机的安全性进行研究与测试。最早开始对可靠性进行研究是 20 世纪 40 年代的美国,他们投入大量的人力物力,将研究应用于电子元器件中,取得很大的成果,开创了这一领域。而在随后的50 年代,美国开始有计划地研究可靠性的问题,他们将研究成果应用于导弹系统方面,以增强实力,在复杂的电子系统也同样应用这样的成果。在第二次世界大战期间,由火箭专家 R.Lusser 带领计算出了 V-II 型火箭诱导装置的可靠度。美国也应用这一理论对B-29 飞机的飞行进行可靠性分析。1952 年,美国电子设备可靠性咨询小组通过大量的实验,总结出全新的分析方法,在很大程度上推动可靠性的研究步伐,而且他们的研究成果应用于多个工业领域。正因如此,ARGEE 研究机构于 1957 年发表的“军用电子设备可靠性”成为可靠性领域的“里程碑”,推进着相关基本理论的进展,并逐步走向规模化。
.........
第 2 章 结构可靠性的基本概念
结构的可靠性为在规定的时间(此为广义的概念,包括使用时间、有效时间)和规定的条件(使用方式、环境因素、操作人员水平等因素影响)下,结构完成规定功能的能力。结构可靠度与上一条概念较相似,是指在规定的时间和规定的条件下,结构完成规定功能的概率[11]。可靠性分析就是系统的响应量满足规定要求的概率分析。
2.1 基本随机变量
结构可靠度理论的产生发展是为了解决工程中那些不确定性(随机性、模糊性等)的问题。不确定性是指事件发生的不确定性。分析与推断这类问题需要用不确定性的方法。目前的结构可靠度理论主要是在随机性下讨论的。分析结构的可靠度需要考虑有关的设计参数。结构的设计参数主要有两类:一是直接施加在结构上的作用或间接造成结构变形的作用(各种载荷);二是结构能够承担载荷的能力。这种能力取决于材料强度、结构特点等。实际上,各参数的数值不是具体的定值,而是具有一定随机分布特性的变量。
........
2.2 结构的极限状态
结构的局部或整体超过特定的状态就不能满足某项功能要求,此状态称为结构的极限状态。极限状态是一种临界状态,它介于失效与不失效之间。分析结构可靠度的依据是结构是否达到极限状态。承载能力及正常使用两种极限状态为极限状态的两种组成形式。承载能力极限状态为结构达到极限载荷或由于形变导致不能继续承载的状态(疲劳破坏、压屈、滑动等)。当结构达到这一状态时,即认为结构处于不可靠状态。正常使用极限状态为结构达到使用的耐用性规定的极限值的状态(正常状态下产生的振动、变形、裂纹等)。
...........
第 3 章 转子系统动力学建模..........17
3.1 建立动力学模型时应遵循的原则 ......... 17
3.2 单元的划分与节点位移向量 ......... 18
3.3 单元的运动方程 ..... 19
3.3.1 刚性圆盘 ...... 19
3.3.2 弹性轴段 ...... 20
3.3.3 轴承单元 ...... 23
3.4 系统的运动方程 ..... 24
3.5 转子系统的固有频率与临界转速 ......... 24
3.6 转子系统的不平衡响应 ......... 25
第 4 章 多盘转子系统的随机响应..........26
4.1 ANSYS 简介 ........... 26
4.2 多盘转子系统的有限元模型 ......... 27
4.3 转子系统的瞬态响应 ........ 29
4.4 转子系统随机响应 ......... 30
4.5 转子系统随机响应灵敏度 ..... 33
第 5 章 多盘转子系统的频率可靠性分析 .....37
5.1 NESSUS 简介 ......... 37
5.2 转子系统的固有频率与临界转速 ......... 39
5.3 转子系统可靠度 ..... 41
5.3 转子系统可靠性灵敏度 ......... 43
第 5 章 多盘转子系统的频率可靠性分析
本章依然以三盘转子系统为研究对象,在 ANSYS 中建立了转子的有限元模型。对三盘转子系统进行模态分析,得到系统的各阶固有频率与临界转速;绘制了系统的Campbell 图。定义转子系统的极限状态方程,应用 NESSUS 计算在多失效模式下转子系统的结构可靠度。采用 Monte Carlo 法进行随机抽样,得到转子系统的各阶固有频率的均值与标准差,并计算出在各激振频率下各参数对系统的频率可靠性灵敏度,研究了随机参数的统计特性对转子系统固有频率的影响规律。
5.1 NESSUS 简介
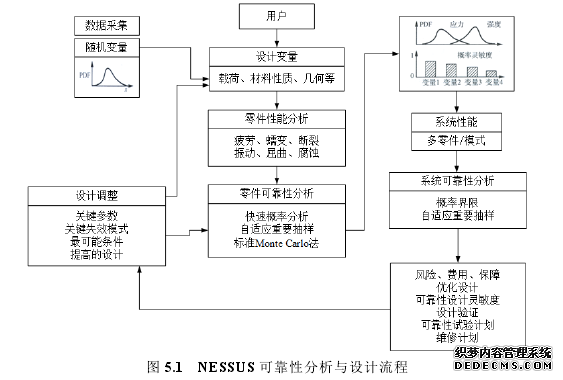
NESSUS 是由美国西南研究所为 NASA 航天飞机主推进系统的概率设计而研发的可靠性分析软件工具。其可以分析多种类型的问题,具有丰富的求解算法以及可靠性问题的定义方式。NESSUS 的最大特点就是可以处理复杂问题的概率求解,包括某些大规模运算,例如有限元分析。原因是该软件可以很容易地建立隐式或显示的功能函数模型,它包含 10 种常用的随机变量分布形式。NESSUS 的分析过程包括了建立状态方程、确定分布类型、随机变量映射到有限元模型中、选取响应量、选择概率分析方法、确定性分析、参数扰动分析、概率分析等步骤,具体流程如图 5.1 所示。NESSUS 的概率计算方法主要有解析法、随机抽样法以及组合法这三大类,在选择方法时,不仅要考虑功能函数、效率、精度,还要依据具体分析目标的实际情况,综合考虑这些影响因素可能对计算的结果的影响。NESSUS 软件具备与目前流行的多种第三方和商业确定性分析软件的接口,包括有限元软件 ABAQUS、ANSYS、MSCNastran、LS-DYNA 等。同时,“用户自定义”模块可以将任何“黑箱”程序与 NESSUS 进行接口。将 NESSUS 与 ANSYS 相结合实际上就是利用 NESSUS 反复调用 ANSYS 的过程。#p#分页标题#e#

..........
结 论
本文在总结了国内、外转子动力学、结构可靠性的研究现状基础上,利用随机有限元法,对转子系统的径向位移的随机响应、系统的频率失效概率及其灵敏度进行了研究。本文首先对转子系统建立了有限元模型,利用 ANSYS APDL 进行了有限元分析,得到了转子系统的固有频率,选择需要进行可靠性分析的工况。在对转子系统进行可靠性分析过程中,结合 ANSYS 与 NESSUS 软件,通过 Monte Carlo 法进行抽样,得到了转子系统可靠性参数,对实际工程应用有重要的借鉴作用。全文的主要工作及得到的主要结论总结如下:
1.针对转子系统的结构特点,对转子系统的模型进行合理的简化。在 ANSYS APDL中建立三盘转子系统的有限元参数化模型。
2.对三盘转子系统进行瞬态分析,得到了转子系统启动时刻的各圆盘质心径向位移。把转子系统的一些参数设为具有一定分布特性的随机变量,通过 Monte Carlo 法进行抽样,得到了各圆盘径向位移的均值与标准差。结合灵敏度技术,得到转子系统各随机参数对圆盘径向位移的响应灵敏度,并绘制了灵敏度曲线。得到圆盘的质量是影响转子系统径向位移的主要因素,其次是圆盘的偏心距,最后为轴承的刚度。
3.在 ANSYS 中对三盘转子系统进行模态分析,得到了转子系统的各阶固有频率与临界转速。利用 MonteCarlo 法进行抽样,得到转子系统各阶固有频率的均值与标准差。根据转子系统的共振失效准则,定义转子系统的极限状态方程。求出转子系统的可靠度。结合 NESSUS 得到转子系统各随机参数的可靠性灵敏度。分析了各随机参数对转子系统可靠度的影响程度。
4.建立双盘转子系统的响应方程,得到系统的前 2 阶固有频率的均值与标准差。根据油膜振荡发生时转子的激振频率与固有频率之间的关系,建立系统的极限状态方程;根据共振转子系统的固有频率与激振频率的关系,建立系统的极限状态方程。考虑两失效模式之间的相关性,计算得到转子系统各随机参数的可靠性灵敏度。通过分析在关键激振频率下的转子系统各随机参数的可靠性灵敏度值,确定转轴长度、弹性模量、转轴直径、与圆盘厚度这些参数对转子系统的可靠度影响是敏感的,圆盘直径与密度是不敏感的。丰富了双盘转子系统的可靠性设计与优化的理论依据。
..........
参考文献(略)

