本文是一篇计算机论文,计算机论文是计算机专业毕业生培养方案中的必修环节。学生通过计算机论文的写作,培养综合运用计算机专业知识去分析并解决实际问题的能力,学有所用,不仅实践操作、动笔能力得到很好的锻炼,还极大地增强了今后走向社会拼搏、奋斗的勇气和自信。(以上内容来自百度百科)今天为大家推荐一篇计算机论文,供大家参考。
第 1 章 绪 论
1.1 研究背景和意义
在工程技术和科学研究领域中,许多应用问题可以归结为数学模型的数值计算问题。由于数值分析理论和方法在实际问题中被广泛应用,所以探索新的数值方法的研究具有重要的现实意义。数值积分是数值分析的重要组成部分,当前数值积分的研究也是非常活跃的研究课题之一。例如在计算机领域中:图像处理问题、网络覆盖连接问题、PIN控制器、连续仿真系统、无网格数值模拟系统等都涉及数值积分计算问题,这一课题的起源可追溯到古代,其中较为突出的例子为:魏晋时期数学家刘徽在计算圆周率时求解圆面积的割圆术。解数值积分问题的方法最初是通过找到被积函数的原函数,再利用 17 世纪出现的牛顿-莱布尼兹公式求解积分值,但是在实际应用过程中,被积函数常常有时无法找出具体解析表达式,或积分原函数十分复杂,此时无法采用牛顿-莱布尼兹公式求解,只能采用近似求解的数值积分方法。17世纪以来,先后出现了梯形求积公式及复化求积公式、抛物线(Simpson)求积公式及其复化求积公式、牛顿-柯特斯(Newton-Cotes)求积公式和高斯(Gauss)求积公式[1-14]等,这些方法都有其自身的优势和局限性,其中梯形求积公式和抛物线求积公式的代数精度分别为 1 次和 3 次的,相对而言其精确度较低;n 阶高斯求积公式代数精度达到 2n+1,精度更高,由于当 n≥6 时,高斯型求积公式的计算量大,在实际问题中使用不便。其中代数精度的提高是数值积分法评估的重要指标之一。随着计算机技术的飞速发展,逐步地计算机智能算法也被数值计算方法所应用,这种方法进行近似求解过程中的特点是计算量低、精度高、收敛速度快等,而且应用领域越来越广,因此数值分析理论和智能算法相结合的相关研究具有重大的研究价值和广泛的使用前景。在工程技术和科学研究过程中,智能算法[15-26]在数学模型优化求解问题中发挥着越来越重要的作用,一些智能算法也逐步在求解数学问题的数值积分法方面被广泛研究和应用,例如:遗传算法[27]、蛙跳算法[28]、神经网络算法[29]、粒子群算法[30]、人工鱼子群算法[31]、蜘蛛优化算法[32]、蝙蝠算法[33]、布谷鸟优化算法[34]、进化策略方法[35]、差分进化算法[36]等在数值积分计算中得到了广泛应用。
...........
1.2 国内外研究现状
在国内外,数值积分求积公式的理论及其应用的研究非常活跃。数值积分的主要研究方向有:(1) 被积函数满足一定条件下,构造积分近似计算的新型求积公式,且进行求积公式的误差估计,并给出相应的优化算法;(2) 基于智能算法理论,优化积分求积公式的算法及其应用问题。
..........
第 2 章 相关知识介绍
2.1 基本概念
在许多工程技术和科学计算过程中,人们常用碰到近似计算求解某类数学模型解积分的科学计算问题。数值积分方法是研究如何利用离散节点函数值来求可积函数积分的近似值。近几个世纪以来,诸多学者建立了多种数值积分方法,其思想为用被积函数在离散节点上的信息来逼近给出定积分的数值计算方法。寻找各种有效的适合计算机编程的数值积分的近似算法在实际应用中具有重要的理论意义和使用价值。另外,在实际问题的研究中,一定的精度限制条件下,人们更注重的是用智能算法求值时的效率问题,用数值积分求解比求原函数解析表达式要有效,而一些研究积分方法过程中面临的问题是要从试验数据而来,那么理论上的积分计算公式就完全用不上了,研究的重点就侧重近似值的误差估计问题。 本文主要研究一元可积函数的数值积分问题,构造了新的求积公式,同时给出了基于智能方法的求积公式算法。本文主要研究一元可积函数的数值积分问题,将构造6个新的复化求积公式,同时研究智能算法在新的复化求积公式中的应用。
...........
2.2 经典求积公式
本节着重介绍经典积分求积公式及其误差估计:梯形求积公式及复化求积公式、抛物线求积公式及其复化求积公式、牛顿-柯特斯求积公式和高斯求积公式[1-14]。本节阐述了当前数值积分求积公式的误差估计的主要研究工作,其中包括:一阶和二阶可微函数的复化梯形求积公式的误差估计、可微函数的积分等式和误差估计、复化抛物线求积公式的误差估计、有连续导数的条件下的求积公式以及最近一些进展工作,其中建立经典抛物线求积公式和梯形求积公式的统一格式、构建新的放宽条件限制的一元积分公式和进一步提高求积精度算法研究都是亟待解决的重要问题。
.........
第 3 章 梯形和抛物线求积公式的统一格式及其复化公式 .......27
3.1 引言 ..... 27
3.2 梯形和抛物线求积公式的统一格式及其误差估计...... 30
3.3 统一格式的复化公式及其误差估计......... 32
3.4 特殊函数在误差估计中的应用.......... 39
3.5 本章小结 .... 44
第 4 章 三个复化求积公式及其智能算法研究.......45
4.1 引言 ..... 45
4.2 中间项系数为 1 的复化求积公式和算法实现....... 46
4.2.1 中间项系数为 1 的求积公式构建及算法实现....... 46
4.2.2 误差估计 .... 48
4.3 中间项系数为 3 的复化求积公式及其算法实现.......... 50
4.4 中间项系数为 4 的复化求积公式及其算法实现.......... 54
4.5 基于智能算法的数值积分应用研究......... 56
4.6 实验仿真 .... 62
4.7 本章小结 .... 65
第 5 章 高阶可微函数的求积公式及误差估计.......67
5.1 引言 ..... 67
5.2 高阶可微函数的第一个求积公式...... 67
5.3 高阶可微函数的第二个求积公式...... 70
5.4 特殊函数在两个求积公式误差估计中的应用....... 72
5.5 实验仿真 .... 78
5.6 本章小结 .... 79
第 5 章 高阶可微函数的求积公式及误差估计
5.1 引言
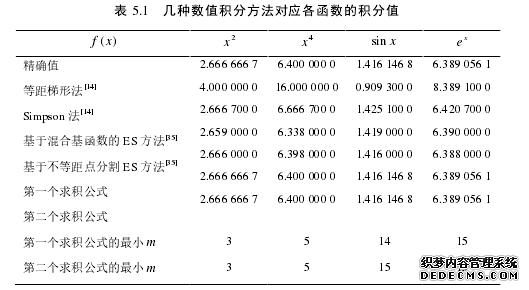
实际问题的数学模型中,有些问题解积分的被积函数为高阶可微函数,在这种情况下仍用常规的经典求积公式来求解积分近似值,有时不能充分发挥被积函数的良好的性质,且有可能导致增加计算量,或降低估计精度,为此,有必要研究高阶可微函数积分的求积公式,且这类问题的研究具有重要的理论意义和广泛的使用价值。被积函数高阶可微时,用 Toylor 级数的部分和来进行逼近,那么用级数部分和进行定积分的近似计算的求积公式,其误差估计条件较强。众所周知,凸函数及拟凸函等函数类在数在数学规划的最优化条件和算法的收敛性判断等诸多问题中有重要的应用,下面主要讨论被积函数微凸函数、凸函数等有关的求积公式的误差估计问题,所建立的结果对求积公式的误差限以及近似计算等工作具有良较好的理论意义和实际使用价值。

..........
总结
在工程技术和科学研究领域中,数值分析理论和方法在实际问题中被广泛应用,而随着计算机技术的飞速发展,计算机智能算法也在数值计算方法中被应用,智能算法进行求解过程中的特点是计算量小、收敛速度快等,因此应用领域越来越广。数值分析理论和智能算法的相结合的应用研究具有广阔的实际应用价值和研究价值。数值积分是数值分析的重要组成部分,数值积分的研究也是非常活跃的研究课题之一。例如在计算机领域中:图像处理问题、网络覆盖连接问题、PIN 控制器、连续仿真系统、无网格数值模拟系统等都涉及数值积分计算问题,但是在实际应用过程中,被积函数有时无法找出具体解析表达式,或积分原函数十分复杂,就无法采用牛顿-莱布尼兹公式求解,只能采用近似求解的积分值方法。17 世纪以来,先后出现了梯形求积公式及复化求积公式、抛物线(Simpson)求积公式及其复化求积公式、牛顿-柯特斯(Newton-Cotes)求积公式和高斯(Gauss)求积公式等,这些方法都有其自身的优势和局限性,但经典求积公式在数值计算中起着重要的作用。随着计算机技术的快速发展,一些智能化算法也逐步在求解数学问题的数值积分法被广泛研究和应用,例如:遗传算法、蛙跳算法、神经网络算法、粒子群算法、人工鱼子群算法、蜘蛛优化算法、蝙蝠算法等在数值积分计算中得到了广泛应用。在实际问题中所遇到的被积函数 f ( x )可能不光滑,甚至并不连续,有时被积函数 f ( x )还会发生振荡,或在某些点无界的情况下,必须考虑一些特殊的处理手段,以适应不同的被积函数 f ( x )在求积区间上出现无界或积分域无界情况,就要对问题进行仔细分析、选择,进而构造出更恰当的积分求积公式。#p#分页标题#e#
..........
参考文献(略)

