本文针对基于差异矩阵的枚举搜索算法存在的缺陷,提出了一种基于向量的 Costas 阵列搜索算法。首先,在判断置换矩阵的同时判断该置换矩阵是否符合 Costas 阵列判断准则,克服了回溯法遍历所有置换矩阵的缺点,去除了不必要的计算,降低了冗余。其次,利用 Costas阵列自身特点,提出了新的基于向量的 Costas 阵列判别准则来判别一个置换矩阵是否为Costas 阵列。即在任意一个 Costas 阵列中没有两个相同的向量。基于向量的算法简化了判决准则,优化了搜索程序,降低了时间复杂度,使得搜索速度得到极大地提升。通过研究双向循环链表和 Costas 阵列的结构特性,利用双向循环链表可以方便的解决生成置换矩阵时多次判断与前几行是否冲突的问题,避免了每次都要与前面的行进行判断比较,有利于程序搜索速度的提升。其次利用 Costas 阵列之对称性来进一步简化搜索程序,加速搜索过程。最后研究了 Costas 阵列的并行搜索,通过并行程序进一步加速阵列的搜索过程,使得搜索高阶Costas阵列也变为可能。本论文主要研究 Costas 阵列的枚举搜索算法以及并行搜索程序,而并行搜索程序依赖于单机性能。在未来的研究中可以进一步研究多机并行搜索,在多机并行搜索中需要将多台计算机通过网络连接以一定的方式有序的组织起来。而这又需要解决网络的连接方式、计算机网络之间通信方式、操作系统、中间件等问题。此外还需研究解决子任务的划分以及各个计算机节点之间的通信协作问题。
..........
第一章 绪论
从上面的内容可以得知 Costas 阵列的应用很广泛,不仅可以用于雷达信号设计、无线通信,而且也可以用于系统的加密等。特别是对于高阶 Costas 阵列,将它们运用到实际中更有意义。由于伽罗瓦域构造法无法构造出特定阶数的所有 Costas 阵列,这使得很多 Costas 阵列不被人发现。这也是本文试图用算法搜索获得 Costas 阵列的目的所在。本文重点讨论了编程搜索特定阶数的所有 Costas 阵列,包括无法用伽罗瓦域构造法构造出的阵列,提出了基于向量的 Costas 阵列搜索算法,同时利用双向循环链表和 Costas 阵列的性质优化了算法的搜索速度,最后通过并行搜索程序加速阵列搜索获得的速度。具体章节安排如下:第一章首先说明了课题探究的背景,同时对国内外研究近况做了简单分析,最后阐述了论文的内容安排。第二章主要介绍了 Costas 阵列和几种获得 Costas 阵列的方式,同时将这些方式进行了比较。第三章提出了一种基于向量的 Costas 阵列搜索算法,改进了置换矩阵生成,同时提出了一种新的 Costas 阵列判断准则,不再使用差异矩阵而是使用向量来对 Costas 阵列进行断。通过对比分析得出该算法明显地提高了搜索获得阵列的速度。
........
第二章 Costas 阵列简介
2.1置换矩阵
矩阵表示法直观明了,但是对于高阶置换矩阵书写不便,同时在利用算法搜索实现中需要大量计算机内存来存储置换矩阵的所有位置上的元素,而其中大部分位置上的元素都0,这样会导致浪费大量的内存,降低算法速度,不利于编程搜索。通过列定位值方法来表述置换矩阵可以很好地解决这些问题。由于置换矩阵的每行中只能有一个位置上的元素是 1,其他位置上的元素都必须是 0。因此只需表示出每行元素 1 在的位置,这样就可以唯一确定一个置换矩阵。
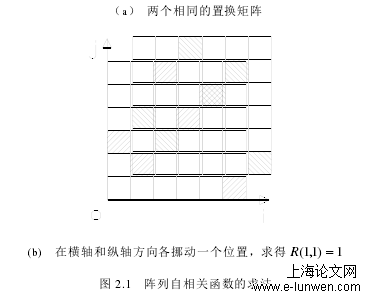

2.2阵列的相关函数
本文通过算法来枚举搜索 Costas 阵列,由于阵列的判定准则对于搜索速度起着决定性作用,因此对于 Costas 阵列的判定准则必须深入研究。根据 Costas 阵列定义可知,对于任何已知阵列,首先是置换矩阵,其次该阵列的自相关函数的次峰值的最大值不超过 1[33]。对于第二个条件目前都是通过差异矩阵来实现对 Costas 阵列的判定[34, 35]。因此,差异矩阵 D 中的列下标是置换矩阵 P 中两个 1 元素位置所在行之间的行差,并且D 中每个非零元是置换矩阵 P 中两个 1 元素所在位置的列之间的列差。由于差异矩阵 D 中的任何一列中都没有一样的非零元,也就是说当置换矩阵 P 的任何两个 1 元素的行相差值致时,列相差值必定不相等,所以置换矩阵 P 为 Costas 阵列。必要性:如果置换矩阵 P 是 Costas 阵列,则在置换矩阵 P 中当 1 元素行相差值相等情况下,列相差值必定不相等。所以差异矩阵 D 中的每一列中都不存在一样的非零元。所以用定理 2.1 可以判定一个阵列是否为 Costas 阵列。如图 2.3(a)中的阵列,其列定位值已求出,计算出对应的差异矩阵,结果如图 2.3(b)所示。由于其差异矩阵中每一中都不存在一样的非零元,因此由定理 2.1 可知,该阵列是 Costas 阵列[36]。
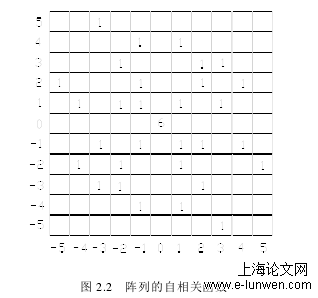

.........
第三章 基于向量的 Costas 阵列搜索算法.................... 15
3.1置换矩阵生成................................................... 17
3.2Costas 阵列判断准则优化................................. 18
3.3算法思想........................................................... 20
3.4结果分析........................................................... 21
3.5本章小结........................................................... 22
第四章 Costas 阵列搜索算法的优化............................. 23
4.1链表................................................................... 23
4.2算法思想........................................................... 28
第五章 Costas 阵列并行搜索......................................... 35
5.1并行程序设计基础........................................... 35
5.2Costas 阵列并行搜索实现................................. 44
5.3结果分析........................................................... 45
5.4本章小结........................................................... 46
.......
第五章 Costas 阵列并行搜索
5.1并行程序设计基础
前面两章已经提出两种加速 Costas 阵列搜索速度的算法,但是这两种算法仍然是串行算法。串行顺序程序中只要程序的输入是相同的,控制线路和最终输出的结果毋庸置疑,必定是同样的,不管程序在哪台计算机上执行。并行是指在含有多个核心的中央处理器,或者含有多个单核的心中央处理器,或者多台计算机上同时完成同一件事情。在执行这些工作任务期间,任何时候都会存在执行多个操作,除非某些任务因为某种原因没有同步执行。只要是同时运行的,就可以称之为是并行的。通常并行的目标是,将本来可以顺序执行的操作,分解成多个可以同时处理的子操作。把这些子操作分布到多个中央处理器执行单元上,使其同时执行,以加快执行速度。一个任务能否被分解以及如何分解,是并行计算理论所研究的问题。因此,本章研究的重点就是 Costas 阵列的并行搜索算法。
5.2Costas 阵列并行搜索实现
由于 Java 高级程序语言拥有许多其他编程语言不具备的特点,使其在全球的使用率仅次于 C 语言。其中一个特性是其包含多线程并行和线程池的类库,因此我们能够轻松实现行程序。所以我们选择 Java 语言来实现 Costas 阵列的并行搜索算法[67, 68]。并行搜索算法我们需要解决的问题是线程频繁创建销毁引起的开销、并行程序在共享变量引起的数据竞争。线程频繁创建销毁问题我们可以通过线程池技术来解决[69, 70],通过线程池可以重复利用已经创建的线程,降低资源消耗,提升 Costas 阵列搜索速度。由于共享变量引起的数据竞争可以通过CAS 来实行原子操作,避免多线程并行造成数据错误。
.........
参考文献
[1] Costas J P. Medium constraints on sonar design and performance[C]. IEEE TRANSACTIONS ON
AEROSPACE AND ELECTRONIC SYSTEMS. 345 E 47TH ST, NEW YORK, NY 10017-2394:
IEEE-INST ELECTRICAL ELECTRONICS ENGINEERS INC, 1975, 11(5): 973-973.
[2] Costas J P. A study of a class of detection waveforms having nearly ideal range—Doppler ambiguity properties[J]. Proceedings of the IEEE, 1984, 72(8): 996-1009.
[3] Moreno O, Omrani R, Maric S V. A new construction of multiple target sonar and extended costas arrays with perfect correlation[C]. 2006 40th Annual Conference on Information Sciences and Systems. IEEE, 2006:512-517.
[4] Golomb S W, Gong G. Signal design for good correlation: for wireless communication, cryptography, and radar[M]. Cambridge University Press, 2005.
[5] 李艳春. 多值逻辑函数组的置换[D].湘潭大学,2006.
[6] Titlebaum E L, MariC S V. Multiuser sonar properties for Costas array frequency hop coded signals[C].International Conference on Acoustics, Speech, and Signal Processing. IEEE, 1990: 2727-2730.
[7] Proakis J G, Salehi M. Digital communications[M]. New York: McGraw-hill, 2001.
[8] Golomb S W, Taylor H. Constructions and properties of Costas arrays[J]. Proceedings of the IEEE, 1984,72(9): 1143-1163.
[9] Beard J K. Costas array generator polynomials in finite fields[C]. 2008 42nd Annual Conference on Information Sciences and Systems. IEEE, 2008: 1246-1251.
[10] Drakakis K, Gow R, Rickard S, et al. On the maximal cross-correlation of algebraicallywww.zhonghualw.com constructed Costasarrays[J]. IEEE Transactions on Information Theory, 2011, 57(7): 4612-4621.
[11] 姚啟航, 李艳玲, 姚建国. Costas 序列穷举搜索算法的研究[C]. 2013年全国无线电应用与管理学术会议论文集. 2013:322-335.
[12] Arce-Nazario R A, Ortiz-Ubarri J R. Enumeration of Costas arrays using GPUs and FPGAs[C]. 2011International Conference on Reconfigurable Computing and FPGAs. IEEE, 2011: 462-467.
[13] 姚建国,王玉峰,衡伟,李艳玲.基于Welch Costas序列的最佳跳频码结构及其在OFDM系统中的应用[J].南京邮电大学学报(自然科学版),2013,33(04):29-38.
[14] 姚 建 国 , 王 玉 峰 , 衡 伟 .Golomb Costas 序 列 的 结 构 及 其 在 OFDM 系 统 中 的 应 用 [J]. 通 信 学报,2013,34(07):1-13.
..........

