本文是一篇计算机论文,计算机俗称电脑,是现代一种用于高速计算的电子计算机器,可以进行数值计算,又可以进行逻辑计算,还具有存储记忆功能。是能够按照程序运行,自动、高速处理海量数据的现代化智能电子设备。(以上内容来自百度百科)今天为大家推荐一篇计算机论文,供大家参考。
第一章绪论
微电子技术和半导体技术经历了分立元件、小规模集成电路、中规模集成电路、大规模集成电路和超大规模集成电路阶段。在其不断地发展过程中,数字应用系统的实现方式也从中小规模标准通用集成电路到用户定制的专用集成电路再到现场可编程器件[2]。在数字电路的设计中,一个布尔函数电路可以用于实现很多其它的布尔函数。布尔函数NPN等价类中所有的布尔函数是相互NPN等价的,通过对一个电路的输入置换、输入非和输出非可以实现布尔函数NPN等价类中其它布尔函数的电路。工艺库中存放了很多标准的电路基元,通过工艺库映射可以将一个布尔函数电路映射到工艺库中的某个或多个电路基元上,即可以采用工艺库中的电路基元来实现一个布尔函数。在该过程中,通过布尔函数NPN等价匹配算法在工艺库中查找这样的电路基元。本文所研究的布尔函数NPN等价分类及等价匹配是为了更好的构建布尔函数的NPN等价分类和速度更快的布尔函数NPN等价匹配算法。
1.1问题定义及其研究意义
从上个世纪30年代开始就有学者意识到了布尔代数在开关电路的分析和综合中具有非常重要的地位[3–5],人们开始研究如何构造一个“好”的布尔网络。作为电路设计与优化中的一项重要技术,布尔函数NPN等价分类和等价匹配也逐步被更多的学者们研究和探索。对一个布尔函数的输入和输出的置换称为P操作,对输入和输出的补运算称为N操作,补运算也称为非运算。根据对输入和输出不同操作的组合,可以得到不同的变换,例如P变换、NP变换、NPN变换等。其中研究最多的是NPN变换,第一个N代表对输入的补操作,P代表对输入的置换操作,第二个N代表对输出的补操作。布尔函数等价分类是将布尔函数划分为多个不同的等价类,每个等价类中的任意两个布尔函数在功能上都是等价的,即对某个等价类中的一个布尔函数的输入和输出执行置换或补操作后可以转换为等价类中的另外一个布尔函数。根据使用变换的不同,对布尔函数的等价分类可以分为多种,例如P等价分类、NP等价分类和NPN等价分类等。因为布尔函数的个数随着变量个数的增加呈双指数增长,所以当输入变量个数增大时布尔函数的分类是一项具有挑战性的任务[6]。布尔函数等价匹配用来判定一个布尔函数与另一个布尔函数在功能上是否是等价的。常见的布尔函数等价匹配有P等价匹配,NP等价匹配,NPN等价匹配和PP等价匹配等。显然,P等价的布尔函数一定NP等价和PP等价,NP等价的布尔函数一定NPN等价。布尔函数匹配的对象可以是不含无关项的布尔函数即指定的布尔函数,也可以是含有无关项的布尔函数;可以是单输出,也可以是多输出的布尔函数。例如文献[7]研究了布尔函数的NPNP等价匹配问题。本文研究了不含无关项的单输出布尔函数的NPN等价匹配问题。
..........
1.2国内外研究现状
1.2.1布尔函数NPN等价分类研究现状
如果两个电路的布尔函数是NPN等价的,那么一个布尔函数电路的实现可以通过对另外一个布尔函数电路的输入和输出增加相应的门来实现。早在上个世纪50年代人们就开始研究布尔函数等价分类问题。对于个变量输入,可以产生22个不同的布尔函数。随着输入变量个数的增加,分类的个数增长很快。所以,目前的研究主要集中在1-6输入变量布尔函数的NPN等价分类。早在1955年,Slepian在文献[18]中采用群论方法研究了布尔函数的NP等价分类。将对输入布尔函数的输入执行的置换操作和补操作构成一个有限群,这个有限群同构于超八面体群。Slepian通过群理论推导出了计算布尔函数NP等价类个数的公式,并计算得出了1-6输入布尔函数的NP等价分类个数。文献[20]计算了4变量布尔函数的NPN等价分类个数。到了1999年,基于文献[20]对布尔函数NPN等价分类的研究,文献[21]和[22]分别提出了根据Reed-Muller重量计算布尔函数分类的方法,他们研究并证明了在对一个布尔函数的输入变量执行置换和补操作时,布尔函数FPRM扩展式中乘积项的个数及具有相同重量乘积项的个数是不变量,由此得出一种新的布尔函数NPN等价分类方法。但是,Dautovic在文献[23]中对于文献[20]中的三个结论提出了质疑,并进行了详细的讨论及说明。文献[24]采用布尔函数的BDD形式,根据P等价的布尔函数具有相同门级电路实现和NPN等价布尔函数具有相似的门级电路实现来判别两个布尔函数是否属于同一个等价类,并采用该方法计算了1-4输入布尔函数的P等价类个数和NPN等价类个数。Anderson在文献[25]中研究了基于谱的等价分类方法,通过对谱特征的研究完成了1-6变量布尔函数NPN等价分类。文献[26]研究了布尔函数等价分类、布尔函数加密等多项关于布尔函数的应用问题。文献[27]通过矩阵运算设计并实现了NP等价分类、NPN等价分类计数算法。鉴于输入变量个数大于6时布尔函数的个数非常多,对布尔函数NPN等价分类结果主要集中在1-6个输入变量。文献[6,28]研究了基于正规式的布尔函数等价匹配算法并对布尔函数进行了分类,但是作者只对很小一部分输入变量个数为6、8、10、12、14和16的布尔函数进行了分类。
.........
第二章布尔函数NPN等价分类及等价匹配的基础知识
在布尔函数等价分类中,类的数量描述了分类准则的强度。类的数量越少,意味着更多的布尔函数可以用一个布尔函数来代表,分类准则就越强。采用枚举方法的布尔函数分类是一项困难且耗时的工作,因为个输入会带来22个布尔函数。本章介绍了使用群代数理论解决布尔函数NPN等价分类问题所使用的理论基础知识及布尔函数NPN等价匹配的基础概念。
2.1Po′lya定理介绍
1933年匈牙利数学家Po′lya将母函数和群论结合在一起形成了一个定理即Po′lya定理,该定理成为了组合数学中解决计数问题的一个重要手段,本节介绍了Po′lya定理相关基础知识。Po′lya定理可用着色模型来描述,设有个着色对象,用种颜色对这个对象的一种着色称为一种着色方案。设是着色对象上的置换群,若一种着色方案能由另一种着色方案通过中置换而导出,则这两种着色方案在本质上是一样的。根据Burnside引理可知同一等价类中的所有元素及着色方案本质上是相同的,而处于不同等价类中的两个着色方案在本质是不同的,因而不同的等价类个数就是本质上不同的着色方案数。
.........
2.2布尔函数的表示形式
布尔函数描述了如何基于对布尔输入的某种逻辑计算并确定布尔输出值,它们在复杂性理论问题和数字计算机的芯片设计中扮演基础角色。布尔函数也称为开关函数,一个布尔函数也可以用一个命题公式来表示。二叉决策图(BDD)表示布尔函数的另外一种方式,是对布尔函数的一种压缩表示方法[120,121]。它是一种基于Shannon扩展(ShannonExpansion)的有向无环图,实质上也是对布尔函数的化简。1986年,Bryant在文献[122]中提出了有序二元决策图OBDD,它是按照变量固定顺序根据Shannon分解的有向无环图。删除布尔函数OBDD中左右分支相等的节点,并且复用相同部分的OBDD为ROBDD。本文算法中采用BDD方式表示布尔函数,BDD的压缩算法可以将BDD中节点所需的空间减少至1到2个比特[123]。论文中的算法在具体实现时采用了Buddy格式描述布尔函数的BDD结构。
.........
第三章基于群代数的布尔函数NPN等价分类研究............24
3.1置换映射......24
3.2非映射........26
3.3布尔函数NPN等价分类.....28
3.4布尔函数NPN等价分类结果.............33
3.5本章小结......38
第四章基于结构化特征的布尔函数NPN等价匹配算法........39
4.1基本概念与问题陈述.......39
4.2基于SS向量的布尔函数NPN等价匹配算法............46
4.2.1SS向量更新..........46
4.2.2搜索变量映射........48
4.2.3NP变换探测..........51
4.2.4匹配算法............54
4.3实验结果及分析............58
4.4本章小结......65
第五章基于结构化布尔差分特征的布尔函数NPN等价匹配算法............66
5.1Shannon余子式的运算......66
5.2结构化差分特征............68
5.3基于SDS的布尔函数NPN等价匹配算法...71
5.4实验结果及分析............78#p#分页标题#e#
5.5本章小结......80
第六章 一种基于正规式的布尔函数NPN等价匹配算法
正规式是布尔等价类中的代表,在工艺库绑定过程中,将工艺库中电路基元的正规式存储在哈希表中。当对电路函数 执行工艺库绑定时,计算布尔函数 的正规式并进行哈希查找。如果找到,那么布尔函数 的电路可以被工艺库中的基元实现。基于正规式的布尔匹配算法中,用的最多的正规式是等价类中具有最大或最小真值表的布尔函数,本文介绍了一种新的正规式。
6.1特征与特征向量
通常,一个特征也称为过滤器或必要条件,它们是布尔函数关于某个或某些变量的特殊属性,与布尔函数的一个或多个输入变量有关。关于一个变量的属性被称为1-阶特征[1]。例如在第三章中提到Shannon余子式的可满足项个数。通过1-阶特征可以区分变量,因为布尔函数的输入变量置换后其1-阶特征不变。也就是说,两个布尔函数之间输入变量的任何可能的关系都被限定在具有相同的1-阶特征下。所以,如果一个布尔函数的每个变量都有不同的1-阶特征,那么它与其他的布尔函数的变量之间的可能关系至多只有一个。这就是为什么将1-阶特征作为识别变量的标识。对于任意 变量布尔函数,每个变量的1-阶特征构成一个特征集合。尽管1-阶特征集合可以用于识别变量,但是大部分布尔函数中都会有多个变量具有相同的1-阶特征值。至今,没有任何一个1-阶特征集合可以唯一的识别所有的变量。因此,需要使用高阶特征及其它特征来实现这个目标。
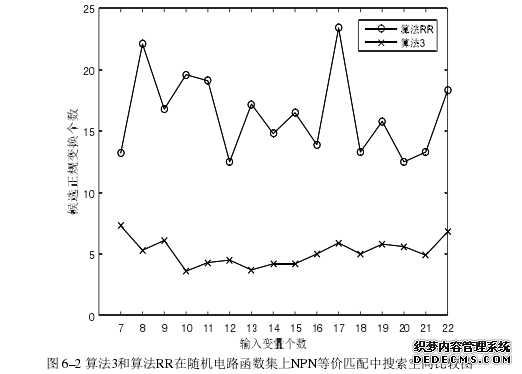

.........
总结
本文重点研究了逻辑综合中的布尔函数NPN等价分类与等价匹配问题,论述了如何利用群代数理论解决布尔函数NPN等价分类及如何利用布尔函数的特征解决布尔函数NPN等价匹配问题。通过研究推出了一种新的计算布尔函数NP和NPN等价类个数的方法,显著地减少了NP和NPN等价分类计数的计算复杂度。论文设计了三种布尔函数NPN等价匹配算法,提出了新的组合特征及新的正规式,减少了NPN等价匹配的搜索空间并提高了匹配速度。论文所完成的主要工作及内容总结如下:
1.布尔函数NPN等价分类与等价匹配在逻辑综合中有着广泛的应用,本文在阅读了大量的相关文献后,分析总结了现有的NPN等价分类方法及成果。详细介绍了目前主要的NPN等价匹配方法,总结了NPN等价分类与等价匹配相关的基本数学方法及基本概念,确定了本文研究的方向,为后续的研究工作提供了理论的支持。
2.针对布尔函数NPN等价分类问题,在对群代数理论学习的基础上,结合NPN等价分类特点,提出了新的布尔函数NP和NPN等价分类方法。论文研究了P群和N群的性质,结合Burnside引理和Po′lya定理在解决 种颜色对 个物体不同着色方案计数问题上的应用,将布尔函数NP等价分类转换为2种颜色的着色方案计数问题。利用布尔函数NP等价分类计数方法与母函数的结合推出了计算NPN等价类个数的方法。论文利用GAP(Group, Algorithm, Programming)工具和相应的计算公式计算出了3-10变量的NP和NPN等价分类计数结果。
..........
参考文献(略)

