本文是通信工程论文,此外,我们通过全局优化和使用新型四强度方案等方式提升其性能。此时,在传输数据量比较少的时候也能有较好的传输距离和码率。这种光源在理论中展示出了较大的优越性,而其结合MDI-QKD的实验实现以及实用化也将是值得探索的领域。在这过程中还存在如下的一些挑战:首先,MDI-QKD的核心技术要求保证较高的双光子干涉可见度,对于HSPS来说,标记后的干涉可见度取决于非线性晶体的纯度,即参量下转换产生的一对光子之间是否存在频谱关联。这对晶体的设计提出了较高的要求,如何在不使用窄带滤波器的情况下,得到较高的干涉可见度是一大挑战。其次,由于参量下转换是一个概率性的非线性过程,想要获得较高平均光强的HSPS需要造价较昂贵的大功率激光器。降低成本,实现泵浦激光器的小型化是未来实用化进程中的一大挑战。随着未来技术的发展,上述问题能够逐一解决的话,HSPS将会成为MDI-QKD应用中性能较优的实用化光源。MDI-QKD享有测量设备无关的安全性,另一方面态制备的误差造成的漏洞可能会被窃听者利用,从而影响安全性。我们在之前工作的基础上提出了三态无需编码监测的MDI-QKD实用化方案,通过利用不匹配基的数据,原始方案中的完美态制备的要求,可以降低到制备的态在二维希尔伯特空间内。该方案X基下仅需要制备一个态,并且基于更紧致的相位估计方式,我们获得了更好的码率。此外,我们搭建了实验平台对该方案进行了原理性验证。
.......
第一章绪论
量子力学基本原理保证了QKD的理论上的安全性,但其实际应用中的性能尚待提升,以满足多样化需求,部分实际器件存在的安全性问题亟待解决。对此,本文重点研究了测量设备无关协议实际应用中的性能提升、编码误差分析、参考系无关协议优化和发或不发协议适应非对称场景的应用,具体章节的主要内容和安排如下:第二章首先介绍了主流的QKD协议以及实际应用中系统的组成。接着,针对光子数分离攻击和针对探测端的攻击,介绍了诱骗态方法和测量设备无关协议。第三章首先介绍了标记单光子源的产生以及优越性,并研究了该光源结合测量设备无关协议在考虑统计起伏情况下的性能。接着,针对实际情况下的光源起伏的缺陷给出了相应的建模和分析。此外,本章还介绍了据此搭建的实验平台,进行了原理性验证实验,实现了170km的传输距离。第五章介绍了参考系无关协议的原理,并结合测量设备无关协议,给出了协议流程和参数估计。接着,针对参数估计较差和受统计起伏影响严重的问题,给出了改进的诱骗态方案。最后,基于光纤平台,进行了无偏转情况下的实验验证,实现了200km的传输距离。第六章首先介绍了广受关注的双场QKD协议的内容及近期相关进展。接着,针对发或不发协议非对称信道场景应用研究的空缺,本章经公式推导,建立了该协议的普适模型,同时适应非对称和对称情况,提升了该协议的实用性。
......
第二章量子密钥分配背景知识介绍
2.1QKD协议简介
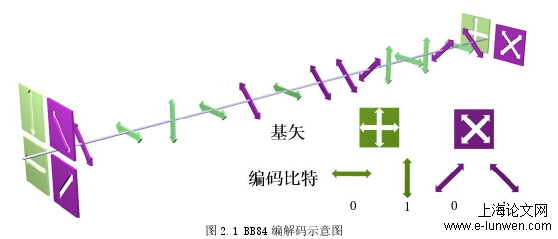
由于在整个过程中,虽然经典信道被认为是不安全的,但由于从未出现过任何的与比特相关的信息,仅公开了基矢,因此保护了密钥的私密性。此外,由于单个光子不可分割和不可克隆原理,攻击者Eve将无法通过截获的方式,事先知道正确的基矢进行测量,且被截获的单光子将被用户视为在信道中损耗掉了,不会参与到生成密钥的过程。如果考虑Eve采取截取重发的策略,即对Alice的光子截取并进行测量后,再根据测量结果发送一个虚假的态给Bob.此时,Eve由于不知道Alice选择的基矢,那么他将有50%的概率选错,如果此时Bob与Alice对基成功,那么Bob又将有50%的概率得到与Alice不一致的密钥.在这种情况下,只要随机的选取一定位数的密钥进行对比,就可以发现其中误码率的升高,总体来看将存在50%´50%=25%的误码,与不存在窃听者接近0误码的情况相差较大,即可发现窃行为。最后,为了提高方案的实际性能,进一步引入了新型四强度方案,降低了统计起伏影响,提升了参数估计的准确性。第四章首先介绍了态制备误差存在的影响,以及相关的损耗容忍方案。在此基础上,介绍了改进的无需编码监控的方案,有效的提高了该方案的性能
2.2QKD协议的安全性基础
QKD协议在安全性证明时都会对实际的设备做出一些假设,但一个实际的系统永远不能做到完美无缺。在攻击时,窃听者需要想尽办法获取超过通信双方所认为的他能够获取到的信息量。既然QKD的理论安全性是基于量子力学,那么唯一的能够做到获得更多信息的情况就是在用户双方这些假设不成立的时候。下面我们将介绍一些常见的实际情况下的缺陷和相应的攻击手段。图2.3展示了使用诱骗态前后的密钥率差异情况,可以看出,基于GLLP公式,诱骗态方法可以极大地提升传输距离和密钥率。上文中指出,在不使用诱骗态时GLLP密钥率与信道穿透率的平方成正比。而使用诱骗态方法后,又回到与使用单光子源的方案一样的水平,即与穿透率的一次方成正比。用诱骗态方法时,除了主动调制诱骗态的方法,研究人员还提出一种被动式诱骗态的方法[42]-[44]。区别于主动式诱骗态利用强度调制器等设备主动地调节光强,被动式诱骗态利用Alice端本地探测器的触发事件和非触发事件的统计概率等价于不同光强得到的光子数分布概率。这种被动式的方法可以免疫强度调制器不完美引入的光强起伏或一些侧信道漏洞等,具有一定的实用价值。
第三章标记单光子源MDI-QKD协议的实用化研究..................................................................23
3.1标记单光子源.....................................................................................................................23
3.2基于HSPS的MDI-QKD的统计起伏分析.....................................................................25
第四章无需编码监控MDI-QKD的性能提升与实现..................................................................44
4.1改进的无需编码监控的测量设备无关协议.....................................................................44
4.2原理性验证实验.................................................................................................................50
第五章改进的参考系测量设备双无关协议..................................................................................61
5.1参考系无关协议.................................................................................................................61
5.2参考系测量设备双无关协议.............................................................................................62
5.3改进的参考系测量设备双无关协议.................................................................................64
.........
第六章实用化非对称发或不发量子密钥分配协议研究
6.1双场QKD协议简介
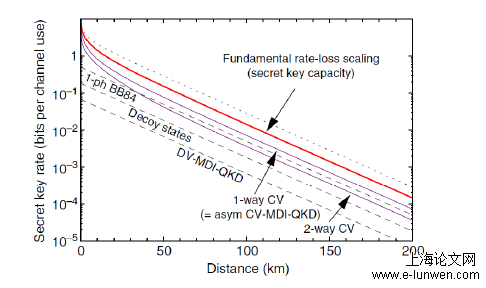
目前已经有不少小组实现了TF-QKD类协议的实验:Minder等人针对原始TF-QKD和SNS-QKD实验进行了原理性验证[124],实现了90dB衰减下的传输,部分数值超过了PLOB界;Wang等人基于Cui的方案实现了300km低损耗光纤下的传输,超越了PLOB界[125]。Liu等人基于SNS-QKD的方案结合主动奇宇称配对的方法[126],实现了509km的光纤传输[127][128],其实验结果超越了绝对的PLOB界;Fang等人基于相位匹配QKD的方案实现了502km超低损耗光纤的传输[129]。Zhong等人利用Sagnac环型结构实现了Curty等人方案的原理性验证[130]。在众多理论协议和实验验证中,SNS-QKD以其能够容忍较大误码的优势吸引了众多关注[131]-[136],在下面一小节,我们将研究该方案适应非对称情况的模型。通过构建新的约束条件,原始诱骗态协议能够继续适用于该方法。该普适模型既可以兼容信道对称的情况,也可以适用于非对称情况。仿真结果表明,该方案较原始弥补信道差值的方法,在传输距离和码率上都有了显著的提升。
6.2非对称发或不发量子密钥分配协议
但是这种方案仍存在一个问题,目前的理论都是假设两个用户到中间节点的距离相等,如果此时面对的是一个距离不相等的情况,继续使用原始模型,那么随着非对称程度的增加,码率将急剧下降。此时一种做法是将距离近的用户在本地加入光纤,弥补成对称方案。这时原始对称协议模型完全适用,但是码率会因为额外光纤的加入而降低。真实的用户网如图6.3(a)所示,此时几乎所有用户都按照最远的距离去弥补衰减,该情景就像“木桶效应”一样,短板决定了整个系统的下限,从而大大降低了系统的整体性能。此外,图6.3(b)所展示的这种利用卫星作为中间节点的轮船之间的通信,由于轮船会一直移动,到中间节点的距离也在变换。如果采用弥补光纤的方法,那么这个光纤的长度也需要不停的变化,这对系统带来了极大的不便。在理论研究比较成熟的MDI-QKD协议中,已经有相关工作对这种非对称的情况进行了讨论[138]-[140],他们通过对不同基矢下性能的分析,并对光强等进行独立的优化,从而提出了不弥补损耗的改进方案。在之前一些SNSTF-QKD协议实际条件下的相关研究中[131]-[133],都假设用户双方到中间站距离相等,而缺少对上述非对称情况的分析。在这里我们首次针对TF-QKD类协议中的SNSTF-QKD协议提出了其非对称情况下更普适的模型。与MDI-QKD协议非对称情况不同的是,此时的诱骗态方法不能直接使用。经过分析和重新推导后,我们的对其加入光强比值的约束条件,使得诱骗态方法能够重新适合该模型。
........
第七章总结与展望
由于协议和实验装置设置的优越性,我们实现了100km和170km光纤下的传输。较之前同等安全性的方案,该方案在传输距离上是最远的。本RFI-MDI-QKD在拥有非常好的安全性和实用性,但之前的相关方案基于诱骗态的参数估计给出的结果比较差,主要问题在于采用了三种强度,并且每种强度在各个基矢下都进行制备。此时优化参数时,信号态既要承担参数估计的任务,又要进行成码。而改进后的方案,信号态仅在Z基下制备,主要负责生成密钥,诱骗态仅在X和Y基下制备,负责参数估计,避免了优化时相互掣肘的情况。本方案在参数估计时吸取了MDI-QKD参数优化的经验,并且考虑了基矢之间的组合关系,最终实现了理论方案性能的优化。此外,基于第四章类似的装置方案,实现了RFI-MDI-QKD原理性验证实验,验证了偏转角为0的情况,实现了200km的传输距离。在未来进一步的研究中,该实验系统还需进一步提升,做到随机调节光强和相位,实现真正的无需参考系校准的方案。TF-QKD的提出打破了不使用量子中继情况下的信道容量界限,在传输距离上有明显的优势。其变体协议中SNSTF-QKD因其能够容忍较大的本底误码受到了广泛的关注。在实际组网中,用户在这种依靠中间站进行测量的QKD协议中很难关于中间节点对称。因此,我们提出了SNSTF-QKD普适的模型。该模型的提出,提升了SNSTF-QKD协议的实用性和组网中的适应性。此外,该非对称协议的分析方法也对其他TF-QKD变体协议具有重要借鉴意义。
参考文献(略)

