实验论文怎么写哪里有?本文通过 PIV 与 BIV 结合的方法,对溃坝波运动内部流场进行测量研究,通过内部流场进一步分析溃坝波掺气运动特征。主要成果及结论如下: (1)首先根据 PIV 及 BIV 技术的原理,结合实验室实际情况搭建了一个生成溃坝波的实验平台,通过利用同步器与电磁铁控制重物下落的实验设计,提高溃坝波生成的同步性。经过 20 次实验重复测量的结果表明,速度矢量较为平滑,实验结果已经足够收敛,实验具有较好的重复性和可靠性,满足取系综平均时的可重复性要求。
1 绪论
1.2 国内外研究现状
1.2.1 溃坝波理论研究现状
溃坝波最早的理论研究可以追溯到 19 世纪。1871 年,圣维南(Saint-Venant)提出描述浅水体中非恒定渐变水流运动规律的偏微分方程组,命名为圣维南浅水方程组,为此研究方向奠定了理论基础。1892 年,Ritter 基于圣维南(Saint-Venant)浅水方程,首次用特征线法推导出了上游无限长矩形水平干床河道上坝体瞬间全溃的流体运动理论解,通过理论解可以得到溃坝流量、正波与逆波速度、自由表面的高度分布及演化[12]。由于忽略了流体的粘性、河床摩擦力和水体内部的运动,Ritter 理论解与实际情况之间出现明显的偏差[13-14]。
溃坝波运动的影响因素众多不能完全忽略,因此大量的学者基于不同的影响因素进行了许多理论研究。林秉南沿用水平、无阻力、干河床的简化形式,假定河床断面为抛物线,针对坝体瞬间全溃的情况用特征线理论黎曼解法获得了有限长水库的溃坝波理论解[15]。谢任之将河床断面概化为抛物线,得到的近似解析解可以计算瞬间全溃、逐渐溃等不同情况,并归纳出对于水库溃坝流量计算的统一公式[16-18]。伍超按照特征理论将浅水方程转化成黎曼不变量形式后,对被积函数先用级数展开再积分,得到了梯形断面的流速解析表达式[19], 而后用多条折线段来描述一个任意给出的溃坝决口断面形状,提出求解任意决口断面溃坝水力特性的形态参数分离法[20]。宁利中将浅水方程转化成黎曼不变量形式后,对被积函数先用级数展开再积分,得到了椭圆形断面的流速解析表达式[21],而后进一步获得了弧形断面和任意梯形断面无因次水深方程,导出了任意梯形和弧形断面溃坝洪水最大流速和最大流量解析解[22]。Chen 采用尺度变换理论将作为两个自变量的时间和空间坐标替换为一个独立的无量纲相似变量,从而将控制偏微分方程转化为常微分方程组,得到了无摩擦水平河道溃坝波的相似解,针对三角形断面棱形河道,提出了干床溃坝波的解析相似解和湿床溃坝波的多项代数方程[23]。
3 溃坝波流场实验介绍
3.1 实验设备
3.1.1 实验水槽
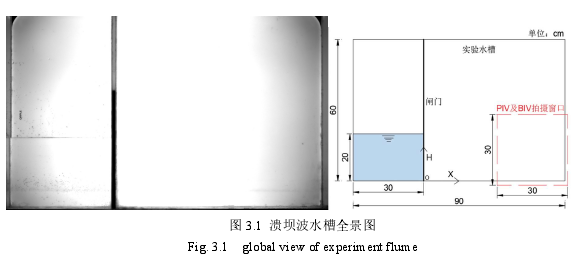
目前对于坝体瞬间全溃的溃坝波的实验过程,通常通过实验室水槽以及安装在水槽中间可以瞬间抽出的防水闸门进行。在水槽中防水闸门的一侧充装一定量的水用以模拟上游水库,防水闸门的另一侧根据情况保持干燥或保持一定水位,以模拟下游干河床或下游湿河床。防水闸门通常用重物下坠或机械控制使之瞬间拉起,当闸门瞬间被抽出,维持上下游水位差的屏障消失,上游水库的水由于重力作用倾泻而下,由此产生了由重力驱动的溃坝波。国内外学者利用闸门瞬间抽出的溃坝波产生装置对溃坝波的各个方面进行了大量的研究,本文在国内外惯用的溃坝波实验装置的基础上,增加同步器控制的重物释放装置,制造了可以在多次重复实验里同时产生的溃坝波,本章将对实验设备、实验布置进行详细介绍。
本实验在大连理工大学海岸及近海工程国家重点实验室进行,使用厚度为 2cm 的高透玻璃制造了一个长 0.9m,宽 0.25m,高 0.6m 的矩形实验水槽。
5 溃坝波流体运动特征分析
5.1 自由表面演化过程
5.1.1 演化过程实验结果
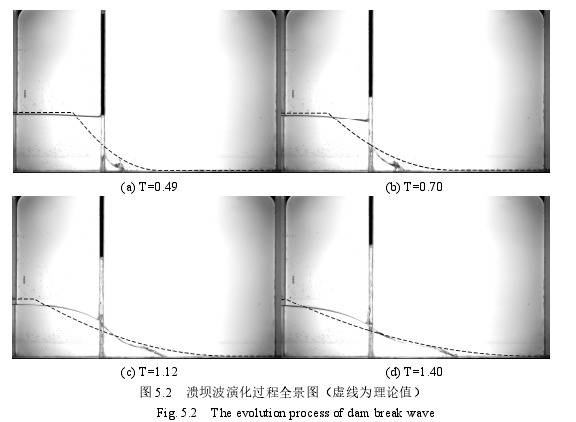
溃坝波自由表面演化过程如图 5.2,闸门平均开启时间为 0.07s,无量纲时间 T=0.49,开启时间符合 Lauber 和 Hager 提出的闸门开启时间临界值标准 T<21/2,可以视为坝体瞬间全溃[13]。实验全景图由 BIV 方法拍摄,图中虚线为理论计算所得的溃坝波自由表面。Ritter 的理论解在闸门上游的自由液面是向下凹的二次函数曲线,且在逆波波尖处不光滑,而本实验的自由液面在闸门上游都向上凸起,在逆波波尖处连续且光滑,自由液面演化规律与 Lauber[13]、Oertel[14]、Lobovsky[40]、Wang[38]等人实验结果类似,与 Ritter 的理论解之间有较大偏差。
溃坝波的初始条件可以作为在一个点产生间断的黎曼问题, Ritter 的理论解即浅水方程黎曼问题的求解。黎曼问题的求解通常假定间断点在初始条件开始之后立即连续,而通过高速摄像机拍摄的结果,如图 5.2(a)、(b)可知,在溃坝发生后,溃坝波在闸门处为不连续的间断状态,经过一段时间后自由表面才逐渐在水平方向变成连续。因此,基于黎曼问题求解 Ritter 溃坝理论解的前提假设与实际情况有差异,间断点由间断变为连续需要一个过程。
5.2 闸门上游流场特征
实验结果表明,闸门附近水体的垂向速度较大,受闸门提升的影响不明显。如图 5.3(a)中所示,闸门提升对水体的影响仅仅局限在一个较薄的流体层中,但由于 PIV 计算窗口宽度大于该流体层的厚度,因此当闸门提升的速度足够快时,该层流体对实验速度矢量计算结果影响较小,可以忽略不计。由于闸门抽取过程对水体整体运动影响可以忽略,故溃坝初期上游演化与理论产生差异的原因并非闸门效应。
在 T=3.50 时,出现远离直墙的射流与飞溅的水滴,导致波面褶皱且没有明显的波面轮廓。随着时间的推移,远离直墙的射流与飞溅的水滴进一步增多,在 T=4.20 时,波面的褶皱演化成向下的尖刺状,这与瑞利-泰勒不稳定性所描述的重流体在轻流体上方因重力驱动产生的复杂现象相似。其中包括尖刺、褶皱和气泡的形成,尖刺一侧亥姆霍兹不稳定性的发展,气泡之间的碰撞与合并,最终形成水滴飞溅、空气夹带和湍流混合[58-59]。
结论
溃坝洪水波作为一种严重灾害性的水体流动现象,一直是国内外水利工程领域非常重要的研究方向。本文通过 PIV 与 BIV 结合的方法,对溃坝波运动内部流场进行测量研究,通过内部流场进一步分析溃坝波掺气运动特征。主要成果及结论如下:
(1)首先根据 PIV 及 BIV 技术的原理,结合实验室实际情况搭建了一个生成溃坝波的实验平台,通过利用同步器与电磁铁控制重物下落的实验设计,提高溃坝波生成的同步性。经过 20 次实验重复测量的结果表明,速度矢量较为平滑,实验结果已经足够收敛,实验具有较好的重复性和可靠性,满足取系综平均时的可重复性要求。
(2)在将 PIV 及 BIV 技术测量的结果结合的过程中,本文提出基于人工智能的气泡区域识别方法,通过 BP 神经网络、卷积神经网络等不同的识别方法进行综合比较,卷积神经网络的准确率最高,识别准确率达 99.78%。并基于 MATLAB 平台开发出相应的人工智能识别软件,在实验数据的处理中大大降低人工识别的复杂性和时间损耗,为PIV 及 BIV 结合的技术做出了改进。
(3)针对水平干河床下瞬间全溃产生的溃坝波运动过程,通过高速相机捕捉其演化过程全景,得到水位随时间的变化,并将其与理论解进行对比。结果表明溃坝初期闸门上游根据非线性浅水方程得到的理论解与实验结果有一定的偏差,偏差随着时间的推移而减小。通过对上游的流场特征分析,上游的偏差来自于溃坝初始阶段垂向速度的存在以及水平速度沿垂线分布不均匀,这与浅水方程的基本假设不符。当时间逐渐推移,垂向速度会不断减小,水平速度分布逐渐均匀,理论解的偏差也随之减小。
(4)结合 PIV 及 BIV 的技术,对水平干河床下瞬间全溃产生的溃坝波砰击下游直墙的运动过程进行了精确测量,获得了溃坝波砰击下游直墙时掺气运动的内部流场。流场结果揭示了溃坝波砰击直墙时的物理现象,溃坝波砰击直墙后波形破碎,水体向上爬高后向上游进行反卷,同时产生各种不稳定的射流与液滴飞溅,反卷时水流主体包裹气体形成一个逆时针的水气两相流旋涡,在爬高和反卷时直墙根部均存在一个运动方向相反,范围相对较小的顺时针低速旋涡,低速漩涡涡量随时间的推移不断减小。实验结果中两个旋涡涡量相差约 2 倍,旋涡所在位置及水体相互碰撞的位置湍流强度相对较高。
参考文献(略)

