第 1 章 绪论
1.1 研究背景与意义
自我国进入新经济时代以来,制造业因其强劲持续的竞争力,构建了可持续发展的经济体系,在其提升自身的知识技术资本和技术创新能力的同时,还吸引着外商投资,调节着国际收支,是国家乃至世界经济发展的主要动力。 然而,现今企业运营所呈现出的复杂性和动态性勾勒出一个新的竞争环境,信息技术地发展、运输费用地降低、市场间障碍地打破,以及其他各种原因都使企业间的竞争不再仅局限于产品本身,而是更为深远。为了增强企业盈利能力、满足目标客户多样化的消费需求、分散企业营运风险,许多制造业企业会选择生产和销售多种类型的产品。此时,企业需要根据市场需要及自身资源情况、技术条件等,决定生产哪些产品、采用何种生产次序,并且确认各类产品的生产过程,使有限的资源得到合理的配置和使用,寻求最佳的产品组合策略,从而实现利润最大化的目标。进行产品组合决策时,涉及的资源主要包括:构成产品的原材料、用于生产产品的机器设备、操作设备器械运转的劳动力以及产品有关的、必需的软硬件等。产品组合最优化不仅可使企业实现收益最大化,还能稳固企业的市场地位,提高其综合竞争实力,实现要素和投资驱动发展模式向创新驱动发展模式的转变。 在产品组合决策优化的相关理论中,约束理论(TOC)是一种新兴有效的管理经营理念,基于该管理理念还提出了有效产出会计(Throughput Accounting, TA)的概念与方法。由于总成本的最小化并不意味着未来总收益的最大化,因此,该理论不再通过不断缩减成本和费用支出以使企业利润增加,而是允许合理数量的库存和运行费用存在,并聚焦于如何识别和突破阻碍系统整体绩效的局部约束,以全新的视角和方式增加企业收益,有利于转变我国制造业企业对资源不合理高消耗的使用现状、提高资源的整体收益率、维系我国制造业全球竞争优势。
..........
1.2 基于约束理论的产品组合决策研究综述
目前,国内外学者对产品组合决策的研究很多,主要方法可归结为线性规划法(LP)、作业成本法(ABC)、智能算法、TOC 法以及上述几种方法相结合的综合算法,但是 LP 和智能算法鲜少单独使用,需要运用其他方法建立的模型求解,也常作为产品组合最终决策方法。而 ABC 也因其本身的局限性,一般需结合其他算法解决产品组合问题。因此,本文主要介绍可独立运用的 TOC 法及相关综合算法研究综述。对于TOC在产品组合决策领域的应用始于90年代,最早由Goldratt[48](1990)提出,即传统 TOC 产品组合算法,用于产生最优产品组合,但是该算法无法为多约束资源问题提供最优解或近似最优解。 TOC 算法确认多约束资源最优解的失败,促使研究者重新定义 TOC 算法以克服该缺点,并且研究出许多新的算法。Luebbe 和 Finch[49](1992)比较 LP 与TOC 后发现,TOC 可和整数线性规划法(ILP)一样产生最优产品组合,但 TOC在解决两类问题时缺乏有效性:一类是给现有生产线增加新的替换产品,另一类是在多瓶颈情况下,TOC 无法达到最优解。ILP 虽然常用于优化产品组合,但需要高水平的专业知识进行公式构建且需大量时间解答,因此,Luebbe 和 Finch 结合 TOC 聚焦五步骤法(FFS)研究出 TOC 启发式算法(TOCh),将产品组合改善过程以一种直观方式呈现出来,相较于 ILP,TOCh 更为简单、直观、容易掌握。Fredendall 和 Lea[52](1997)提出了 RTOC,用于识别多约束下的最优产品组合,这是传统 TOC 产品组合算法无法做到的,他们发现 RTOC 在大多数情况下提供了与 ILP 相同的结果。Hsu 和 Chung[53](1998)基于优势原则算法(dominance rule-based algorithm),将非紧急约束资源分为三个水平,构建出显式算法以解决多约束资源下 TOC 产品组合问题。王福胜、朱凯等[9](2003)建立了基于 TOC的产品组合决策一般数学模型。Aryanezhad 和 Komijan[62](2004)运用举例证明了 RTOC 在某些情况下生成的是非最优解,因此,他们开发了新的优化算法以获得最优解,且结果与 ILP 的结果相同。Sobreiro 和 Nagano[74](2012)基于 TOC和渐缩问题提出了新结构性启发法,该方法在高质量解和 CPU 时间方面优于RTOC 以及 Aryanezhad 和 Komijan(2004)的改进算法。Tanhaei 和 Nahavandi[75](2013)提出了在两种约束资源环境下,决定最优产品组合的启发算法。
..........
第 2 章 理论基础
2.1 约束理论基础
约束理论(TOC)由 Goldratt 和 Cox[47](1984)在其畅销书《目标》中首次提出,是生产方法上的一次主要革新,以最优生产技术(OPT)为基础,是一套瓶颈企业实现利润最大化的生产计划哲学。 根据 TOC,改善整个系统绩效最重要的是致力于解决“瓶颈”问题。瓶颈是指限制系统提高绩效水平、实现其目标的全部约束因子。瓶颈资源也称为约束资源,根据来源可以分为外部瓶颈和内部瓶颈,根据性质可以分为物理瓶颈、市场瓶颈和政策瓶颈。其中,物理瓶颈可以用物理指标衡量,以物质形态呈现,如工作人员数量有限、生产原料缺乏、设备产能不足等;市场瓶颈是指当产品的市场需求不足,出现供大于求的情况,此时,企业需要开辟新市场或开发新产品以打破瓶颈;政策瓶颈则主要体现在企业的管理思想、制度、方法等方面的不合理。制造业企业类似于一个将生产资源转变为产成品的系统,而各产品所需的资源是最关键的因素,生产过程中如果出现某一资源的实际产能等于或少于计划负荷,该资源就会成为整个系统的瓶颈资源,约束着产品的总产量,其余资源则称为非瓶颈资源。
........
2.2 产品组合理论基础
每一家企业都会为客户提供不同的产品,包括所有的产品线和产品项目。而产品组合就是这些产品线和产品项目的组合方式,其中产品线是指产品类别,而产品项目是指每个产品类别里具体的产品,因此产品项目是包含在产品线内的。产品组合通常以如下四个要素来表示:(1) 宽度:是指企业产品组合中产品线总数,产品线数量越多,产品组合宽度越大。(2) 长度:是指企业产品组合中产品项目总数,产品项目总数越多,产品组合长度越大。(3) 深度:是指企业产品组合中,各条生产线中每个产品项目内包含的产品具体的规格、型号、款式等数量,数量越多,产品组合深度越深。(4) 关联度:是指企业产品组合中,每条产品线之间终极用处、销售途径、生产条件等各环节相互关联的程度。
...........
第 3 章 现有基于约束理论产品组合优化算法分析 ..... 18
3.1 TOCh 算法 ...... 18
3.1.1 算法介绍 ...... 18
3.1.2 算例 ...... 20
3.2 RTOC 算法 ..... 21
3.2.1 算法介绍 ...... 21
3.2.2 算例 ...... 24
3.3 TOC 显式算法 ........ 26
3.4 算法总结与分析 .... 36
3.5 本章小结 ........ 36
第 4 章 基于TOC 的TOPSIS 区间数产品组合优化算法构建 ........... 37
4.1 区间数含义及其运算 .... 37
4.2 基于区间数的 TOPSIS 排序法 .... 39
4.3 区间数权重及可能度确定 .... 43
4.4 基于 TOC 的 TOPSIS 区间数产品组合优化算法 ...... 48
4.5 算例分析 ........ 52
4.6 本章小结 ........ 64
第 5 章 案例研究 ..... 65
5.1 企业基本情况介绍 ........ 65
5.2 企业产品组合现状 ........ 66
5.3 算法运用及结果分析 .... 68
5.4 本章小结 ........ 84
第 5 章 案例研究
5.1 企业基本情况介绍
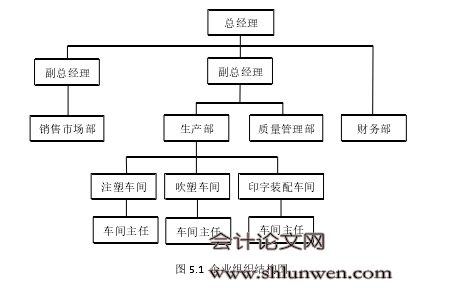
丹阳市某工具包装有限公司 2000 年成立,企业占地面积 5000 平方米,企业组织结构如图 5.1 所示,包括销售市场部、生产部、质量管理部和财务部,其中,销售市场部由一位副总经理监管、生产部和质量管理部由一位副总经理监管、财务部由企业总经理直接管理,生产部包括注塑车间、吹塑车间和印字装配车间。 该企业的主要业务为制造产品工具包装,2010 年开始将汽配产品和附件的新兴产品作为新增点,生产工具包装盒、为外贸企业贴牌的工具组套、汽车配件和塑料轮,其中,工具包装盒包括注塑盒和吹塑盒,汽车配件包括吹塑件、通风管、警示盒和汽车维修工具,塑料轮包括餐车及童车上的吹塑小轮。该企业国内客户按地区分布分别为:江苏省 55%,浙江省 15%,上海市 13%、广东省 5%,其余 12%为欧美地区。该企业主要致力于四种产品的生产和销售,即水壶(BT-150 和 BT-200 两种型号)、通风管(用于黄海 SUV)、工具盒(“1-19pcs”和“15-400pcs”)和塑料轮。水壶用于园艺机,成本及售价均较低,销量高、产量大,适合大批量生产;通风管是企业主要经营的汽配产品,质量要求较低但利润较高;工具盒是企业最为传统和重要的产品,已建立了相当稳定的客户和市场基础,市场需求量大,但成本较高,利润较低;塑料轮用于餐车和玩具车,通用性好,出口偏多,但由于市场竞争激烈且人民币汇率偏高,利润逐年减少。2015 年,每种产品的成本费用基本情况如表 5.1 所示,根据有效产出计算公式可得每种产品的有效产出分别为:2元、14 元、1.2 元和 2.7 元,其市场需求量均为区间数(见表 5.2)。 #p#分页标题#e#

............
结论
TOC 理论可被灵活应用于企业生产管理系统的许多环节,目前已普及全球多个国家,为许多企业,尤其是生产制造业企业带来很大益处,但在我国这一生产制造大国的实际应用并不常见。本文对 TOC 理论及在产品组合中的应用研究进行汇总分析,并介绍了三种产品组合优化算法,基于算法优势和存在的局限性,提出基于 TOC 的 TOPSIS 区间数产品组合优化算法,并通过企业实际应用证明算法有效性。得出以下几点研究结论。
(1) TOC 确实有助于企业决策者改善产品组合现状,提高企业盈利能力,而且已得到广泛应用。
(2) TOCh 算法、RTOC 算法和 TOC 显式算法是目前学术界普遍认可的三种基于 TOC 的产品组合优化算法,各有优势但均存在瓶颈资源只能单个考虑、只适用于精确值的弊端。
(3) 本文构建的基于 TOC 的 TOPSIS 区间数产品组合优化算法,可同时运算几种瓶颈资源下的排产情况且适用于区间数和实数;应用于目标企业中,结合企业生产实际情况后发现,根据运算结果重新安排企业产品排产顺序及产量,能使企业总有效产出显著提高,证实算法是有效可行的。
.........
参考文献(略)

