第一章 绪论
1.1 研究背景
Va R 和 ES,都是测量金融资产和资产组合的市场风险的主要测量工具,在各大金融机构中应用广泛。 金融机构在经济体系中发挥核心作用,因为它们的存在使资金更加具有流动性,成熟性,同时也使风险有效转移。而金融市场与其他市场一样,是一个庞大资金支撑起来的系统,存在着贸易摩擦,并且信息通常不能免费获得。随着金融界的不断发展,各种金融衍生工具层出不穷,由于加入了大量的计量公式,这些金融工具变得越来越复杂。这就需要金融机构通过其掌握的巨大的资金和其所雇佣的高素质员工,在有效地获得信息的基础上,使其业务正常运转。 毫无疑问,一个拥有良好管理系统的金融机构有助于改善整个宏观市场的经济系统,而经营不善的机构则恰恰起到相反作用,为了防止金融机构做出失败的决策并增加金融体系的信心,对金融机构进行某种形式的监管和监督是非常必要的。其中一个最重要的组成部分就是明确哪一个模型是最适合金融风险的测量与监督的。在本文中,我们专注于市场风险模型的选择及其对估计投资组合的风险承受能力的效果。
..........
1.2 文献综述
Va R方法是由1993年被首次提出的。在此之前,金融界已有多种测量市场风险的方法,但是,这些方法在某些方面均有一定的不足。例如,资产负债管理(Asset-Liability Management,ALM)方法过于依赖财务报表分析,因此缺乏时效性;利用β系数及方差来衡量风险只能反映的市场(或资产)的波动幅度,该方法太过于抽象,不直观。而资本资产定价模型(Capital Asset Pricing Model,CAPM)作为一种经典的市场风险衡量方法,无法将金融衍生品揉合到资产组合中,有一定实际操作上的限制性。在上述几种传统方法都无法准确定义和度量市场风险时,通过巴塞尔协会的推广[1],V
a R已成为目前金融界测量市场风险的主流方法。在此之后不到一年,J.P.Morgan就开发出了自己的Va R风险控制估算模型,即我们熟知的Risk Metrics[2],该估算模型因为可以将包含多种金融风险资产的资产组合进行简化,所以被众多金融机构广泛采用,至今仍发挥着重要的作用。 Va R作为一种在银行界被推广多年的风险测度,至今已是广受认可的模型评估方法。对于测量市场风险的Va R模型的能力评估一般通过“回溯测试”(Va R backtesting)完成。它的工作原理如下:我们通过时间t内的市场风险情况(在这里我们用Va R表示)来估计时刻t +1的风险情况,并将其与t+1时刻的真正风险情况加以比较。如果估计值比实际值高,这一天被称看作“异常”,记为“1”,否则,我们会记为“0”,这个过程通常在一个给定的时间长度(通常是几年)内重复多次。“0”和“1”组成的序列应该满足一些统计意义上的假设条件。Kupiec(1995)[3]认为最简单的Va R backtesting 的方法之一就是将实际过程中“1”出现的次数与在一定置信度下计算出“1”应该出现的预估次数进行比较,以此来证明所选择的风险测量模型是否适合测量金融市场风险。并在其文献中提出了一种十分经典的测算Va R模型的方法——似然函数比法(likelihood ratio method,LR)。Berkowitz,Christoffersen和Pelletier(2011)[4]则通过一些进一步的统计检验证明了这一说法。而也有另一批学者从不同的视角对这种方法进行了进一步的完善,其中比较有代表性的是Christoffersen(1998)[5]提出的一种“条件覆盖检验”(conditional coverage test)这种检验方法在原有的基础上加入了对模型的独立性检验法。
...........
第二章 基于 NIG 与 VG 分布的金融资产收益率估计的理论方法
本文分别对 Va R 和 ES 进行建模并进行相关的回溯测试。鉴于我们建模时所需的建模工具大致相同,在对 Va R 和 ES 的实证研究开始之前,我们在本部分先对这些模型进行介绍,具体包括:本文使用的边缘分布函数(NIG 分布和 VG 分布),本文使用的四种 copula 函数以及其三种参数估计方法,本文使用的套期保值公式。
2.1 NIG 与 VG 分布
NIG与VG分布均属于次级莱维过程(subordinated Lévy process)中的一种,不同于正态分布以及Student-t分布等传统分布。NIG与VG分布分别有四个参数,在四个参数受均值、方差、偏度、峰度的影响而不断变化。在模拟分布时,可以随着样本数据的变化而不断改变分布的偏度和峰度,从而与实际情况更好的相拟合。众所周知,由于存在极端价格走势,金融资产的收益率频率分布经常呈现出一种尖峰厚尾不对称的特征,而分别由四个参数决定其形状的NIG与VG分布恰好可以很好的拟合这种状态。
........
2.2 Copula 及其参数估计方法
Copula函数的作用是可以将单个边缘分布连接成二元、三元乃至多元的联合分布。自Sklar(1959)[46]提出“Sklar定理”,copula函数的相关理论也一直在不断的发展与完善,现在已经被应用到多个领域。 而发展至今日,copula函数已经有很多不同的种类。具体来说,可以将这些种类归纳为两大类,一类是椭圆分布族的copula函数(elliptical copula),本文选取的copula函数中,正态copula和学生t-copula(Student-t copula)函数均属于此类;另一类是阿基米德分布族的copula函数(Archimedean copula),本文使用的Gumbel copula和Clayton copula函数均被包含在其中。 在本部分,我们将介绍以上四种 copula 函数,以及三种 copula 函数参数的估计方法,其中,后两种参数估计方法属于 Mo M 法。
............
第三章 基于 NIG 与 VG 分布的世界主要原油资产及资产组合的 Va R .............. 20
3.1 Va R 回溯测试检验法 ......... 20
3.2 世界三大主要的原油现货和期货资产的 Va R ............. 29
3.2.1 原油现货和期货样本数据的统计特征 .... 29
3.2.2 原油现货和期货资产的 Va R ........ 30
3.3 世界三大主要的原油套期保值资产组合的 Va R.......... 39
3.4 本章小结 ..... 61
第四章 基于 NIG 与 VG 分布的世界主要原油资产及资产组合的 ES ..... 62
4.1 ES 的计算与 ES 的回溯测试检验法 ....... 62
4.2 世界三大主要的原油现货和期货资产的 ES..... 65
4.3 世界三大主要的原油套期保值资产组合的 ES ............ 67
4.3.1 资产组合 ES 的回溯测试步骤...... 67
4.3.2 原油套期保值资产组合的 ES ...... 67
4.4 本章小结 ..... 73
第五章 总结与展望 ....... 75
5.1 论文工作总结 ........ 75
5.2 未来研究展望 ........ 77
第四章 基于 NIG 与 VG 分布的世界主要原油资产及资产组合的ES
本章节我们将先介绍 ES 的两种检验法,然后再进行实证检验。实证部分可以分为两步,我们首先通过比较三种原油期货和现货在 ES 两种检验法下的检验结果,并选择出 NIG 和 VG 分布中比较适合拟合单个资产边缘分布的模型。然后同第三章的 3.3 部分相同,通过 copula 函数与 NIG 和 VG 分布相结合,使用ES 检验法选择最适用于三种原油套期保值资产组合的二元模型。
4.1 ES 的计算与 ES 的回溯测试检验法
在很多人眼中,ES 与 CVa R 是等同的,但从严格的意义上来说,ES 相当于CVa R 的改进版。因为当资产组合的收益的密度函数为离散型时,CVa R 模型不是一致性风险度量模型,而 ES 则很好的避免了这一问题。具体的内容,可以参考 ES 和 CVa R 提出原文献,来比对两者的不同(Acerbi 和 Tasche,2001; Rockafellar 和 Uryasev,2002)[105][106]。 另外,不同于 Va R,ES 的结果有很多实现方法。而在接下来的一部分,我们将着重介绍其中的几种以及本章节的实证部分将会用到的方法。与第三章中的 3.1.1 的位置同理,本部分的 ES 的回溯测试检验法本应该放在本章 4.2 的实证部分中,但是这部分对于 4.1.3 的 ES 的回溯测试检验法有一定的铺垫作用,因此,对单个资产 ES 的回溯测试步骤被放在这里。 在实证研究之前,我们对本章节的 ES 单个资产在实证研究中所涉及的回溯测试步骤进行一个大体的说明: (1)在实证研究中,我们将“估计样本”统一定为 500 个样本收益率数据,将“预测样本”定为 250 个样本收益率数据。然后,我们根据 3.1.1 中单个资产Va R 的回溯测试步骤中的(1)、(2)步,模拟出第一个“估计样本”收益率在NIG 和 VG 分布模型下各自的四个参数。 (2)我们使用已知参数的 NIG 和 VG 分布来估计其在显著性水平 p 下的 Va R和 ES,将其作为第 501 天的 Va R 和 ES 的预测值。其中,Va R 使用我们在 3.1.1中使用过的蒙特卡洛模拟法求得,ES 则是经过公式(4-2)(或者公式(4-3))求得。 #p#分页标题#e#
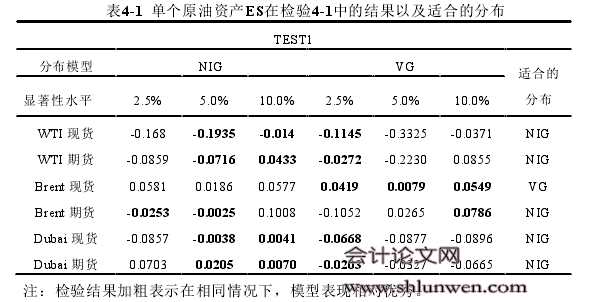

.........
总结
在第三章,采用 NIG 分布与 VG 分布来拟合收益率的分布情况,通过蒙特卡洛模拟法,计算当今世界上最具影响力的三种原油期货——美国西德克萨斯州低硫原油、北海布伦特原油、中东迪拜酸性原油连续期货合约与其对应的现货、套期保值资产组合的 Va R。我们通过大量的实证研究,并使用四种不同的检验方法从各自不同的切入点进行检验。 对于单个资产,我们得出以下结论: 从两种分布对于单个资产的适用性上来看,实证部分说明了在“估计样本”的数据容量一定的情况下,相较于NIG分布,VG分布更适用于计算布伦特原油现货的Va R;而其余五种资产则更加适用NIG分布。 对于资产组合,我们得出以下结论:
第一,从检验结果来看,NIG、VG-copula模型还是比较适用于预测三种原油资产套期保值资产组合的Va R。但是,综合而言,该二元模型对于WTI与Dubai原油Va R的准确程度要远好于Brent原油资产。
第二,我们综合三种回溯测试的检验结果,每种原油都有相比之下最适合其的二元模型。我们将其归纳在表 5-1 中,如果使用某种 copula 参数估计方法估计的最优分布-copula 模型相比之下比较适合于估计某种原油资产的套期保值收益的 Va R,则在表格中填写这种原油的名称,而原油后的括号内表示用于模拟相应的原油现货和期货的最优分布。
.........
参考文献(略)

