本文是金融论文,自从Engle(2002)提出MEM以来,模型的形式得到了极大的丰富和发展,它已经成为了刻画非负值金融时间序列的重要工具,而模型参数估计仍然以MLE为主。可是随着金融市场自动化模式的推广以及计算机技术、电子系统的飞速发展,金融高频数据越来越呈现重尾分布的特征,而MLE对数据的尾部指数敏感,在估计参数时易受数据性质的影响。基于此,本文考虑用稳健估计进行参数估计,克服现有参数估计方法的弊端,并对其理论性质和实际应用进行了研究,现将研究结果总结如下:(1)梳理了近年来MEM的扩展形式,给出了部分扩展MEM的模型形式;(2)提出了参数MEM的稳健估计方法,并在一定的条件下证明稳健估计的相合性和渐近正态性;(3)在误差服从不同重尾分布的情况下,对基于MLE的参数MEM1,1和基于稳健估计的参数MEM1,1进行数值模拟,发现无论样本数据是否重尾以及是否存在异常值,基于稳健估计的参数MEM1,1的估计效果都优于基于MLE的参数MEM1,1;(4)将基于MLE的参数MEM1,1和基于稳健估计的参数MEM1,1运用到大连商品交易所的两只期货进行建模,进一步验证了数值模拟结果,稳健估计的效果更好。
......
第1章绪论
本文的创新点如下:1.对MEM进行极大似然估计时,目前研究的误差分布假定多以指数分布、威布尔分布和Gamma分布为主,大多数模型中比较认可的是Gamma分布,但与误差的真实分布仍存在一定的差距,应该存在其他更适合MEM的分布。本文在已有分布基础上给出了误差项服从Pareto分布的PMEM、Burr分布BMEM和Fréchet分布的FMEM,提高模型数据的适应能力。2.对于MLE的参数估计问题,目前大多数研究主要采取MLE,但是这个方法存在一定的缺陷,在估计金融重尾高频数据时,结果显然还不够稳健。本文首次将稳健估计方法运用到参数MEM的参数估计中,作为模型参数的修正,使得在估计金融重尾高频数据时,结果更加稳健。3.目前研究的对象主要是股市波动率,本文研究了价格极差、成量、成交额指标,还考虑将基于稳健估计的参数MEM应用到期货市场,从LogL和AIC的估计结果来看,基于稳健估计的参数MEM的拟合能力表现得更好。
.....
第2章MEM及其估计方法
2.1参数MEM及其扩展
本章主要从模型设定和估计方法这两个方面阐述MEM的基本理论。MEM是从GARCH模型——ACD模型、CARR模型——MEM这样发展而来的。MEM是GARCH类模型的扩展,同时它与ACD模型具有相似的模型形式和性质,但是它所研究的变量不局限于金融市场交易中的交持续期,而是包括年、月、周、日为频率的时间序列数据和超高频数据。MEM通过对随机扰动项的不同设定可以扩展为不同的模型形式。MEM最常用的估计方法是MLE,我们对其进行简单的推导和解释。最后,我们对稳健估计进行介绍.目前研究的MEM误差分布假设多以指数分布、威布尔分布和Gamma分布为主,且大多数模型中比较认可的是Gamma分布,但这些分布与误差的真实分布仍存在一定的差距。相对而言,误差项服从Pareto分布的PMEM、Burr分布的BMEM和Fréchet分布的FMEM,更适合高频数据尖峰重尾的性质,提高了模型对数据的适应能力。
2.2MEM的参数估计
参数模型一直被广泛地应用于经济领域,相对于非参数模型来说,参数模型形式相对简单,每个参数都有其对应的经济意义,对实际经济数据估计出参数后,模型便于解释,模型估计结果的统计性检验也很方便。MLEMEM中参数估计最常用的方法,当我们知道随机误差项t的分布时,就可以推导出标准MEM的对数似然函数,但是很多金融数据都有重尾的性质,这时MLE结果不稳健。因此本节给出了MEMqp,的稳健估计。MLE方法最早是1821年由德国数学家Gauss(高斯)提出,其主要思想是已知某个随机样本满足某种概率分布,但其中的具体参数未知,通过若干次试验观察出某个参数能使这个样本出现的概率最大,所以把该参数作为估计的真实值。MLE主要步骤就是构造似然函数并对其求解,似然函数是关于模型中待估参数的函数,一般通过样本的密度函数来构造。
.......
第3章理论性质证明及数值模拟....16
3.1稳健估计的相合性...............16
3.2稳健估计的渐近正态性.......18
3.3数值模拟...............................24
第4章期货实证分析........................34
4.1数据选取..............................34
4.2期货价格极差的实证研究...34
第5章总结和展望...........................51
.......
第4章期货实证分析
4.1数据选取
样本选择上,在大连商品交易所中选取了两只规模大、流动性好、行业代表性强的五分钟高频期货交易数据,分别是聚乙烯和聚丙烯。聚乙烯和聚丙烯是重要的塑料原料,占我国树脂消费总量的40%以上。受多方面因素影响,我国聚乙烯、聚丙烯市场动荡不稳,但市场需求量大,国内产量仅占需求量的一小部分。因此,我国的聚乙烯、聚丙烯在相当程度上依赖进口来满足国内需求,造成国内市场受进口数量及价格影响较大,市场不稳。在我国,塑料工业属于朝阳工业,国内包装材料、日用塑料制品等需求强劲,塑料制品应用处于一个高速发展的阶段,推动国内经济发展。聚乙烯和聚丙烯作为塑料市场的风向标,对两者期货市场的研究,有助于预测塑料工业的市场趋势,分析经济发展态势。选取的时间跨度从2017年8月1日到2019年4月30日,数据包含了交易日期、日最高价格、日最低价格、成交量、成交额等期货信息。在这里,我们选取两只期货的三个相同指标,分别是价格极差、成交量、成交额,对两只期货的这三个指标分别进行参数MEM建模,保证了序列为取值非负的时间序列。对数据分析之前,要对原始数据进行预处理:价格极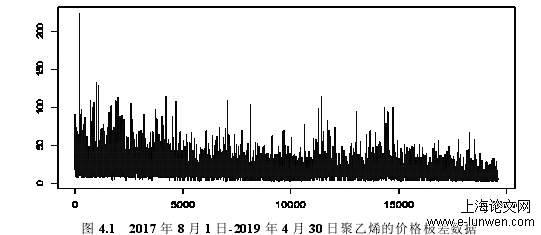

4.2期货价格极差的实证研究
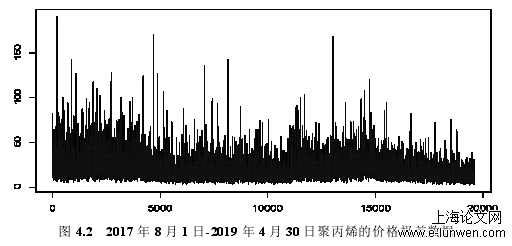
在进行模型估计之前,我们先针对经处理的价格极差原始数据进行统计特征分析,并进行必要的检验。图4.1和图4.2分别为2017年8月1日-2019年4月30日期间聚乙烯和聚丙烯的价格极差数据的变化趋势图,我们可以大致看到两只期货的价格极差波动情况。我们可以发现聚乙烯的价格极差数据普遍大于聚丙烯的价格极差数据,且波动比较小。接下来我们对2017年8月1日-2019年4月30日期间聚乙烯和聚丙烯价格极差的所有样本数据进行描述性统计分析,结果见表4.1。从表4.1中可以看出,聚乙烯和聚丙烯价格极差的均值分别为17.24和18.15,标准差分别为10.51和11.42。这两个指标说明聚乙烯的交易活跃度要大于聚丙烯的交易活跃度。从偏度来看,聚乙烯和聚丙烯的偏度均大于0,这说明两者的价格极差分布曲线均为正偏,因此均适用于非负值模型建模。从峰度来看,聚乙烯和聚丙烯的峰度也均大于3,且聚乙烯的峰度大于聚丙烯,这说明两者的分布曲线均呈明显的尖峰厚尾特征,且聚乙烯的尖峰厚尾特征较聚丙烯更为明显。另外,从表中JB统计量的结果来看,两者Jarque-Bera检验的P值均为0,拒绝了正态性原假设,也说明两者均为非正态分布。我们可以观察两只期货价格极差的直方图和密度估计曲线,更加直观地看出两者是尖峰厚尾的非正态分布,如图4.3和图4.4。

......
第5章总结和展望
MEM和稳健估计的思想提出了基于稳健估计的参数MEM1,1,通过对基于MLE的参数MEM1,1和基于稳健估计的参数MEM1,1进行数值模拟和实证分析,发现基于稳健估计的参数MEM1,1的参数估计效果明显优于MLE,为MEM刻画金融高频数据提供了一种有效的方法。但是受到自身知识和能力的限制,本文还有以下不足:(1)在SM-估计权重的选取上,本文借鉴了其他学者的选取办法。虽然数值模拟和实证分析均已表明S-Huber估计的效果比MLE好,但是如果能尝试更多的权重,也许会有更好的效果。(2)在稳健估计损失函数形式的选取上,本文只选择了绝对值和Huber函数,在以后的研究中可以加入其他的形式,效果可能会更好。(3)在研究对象上,本文仅仅考虑了大连商品交易所的高频数据,今后可以将基于稳健估计的参数MEM延伸到其他期货市场,或者股票市场、期权市场等。
参考文献(略)
参考文献(略)

