本文是一篇金融论文,金融(FINANCE)就是对现有资源进行重新整合之后,实现价值和利润的等效流通。(专业的说法是:实行从储蓄到投资的过程,狭义的可以理解为金融是动态的货币经济学。)(以上内容来自百度百科)今天为大家推荐一篇金融论文,供大家参考。
第 1 章 绪论
1.1 研究现状及意义
1.1.1 研究现状
从 1992 年开始,银行业的利率水平踏上了逐步实现市场化的漫漫征程。同时,央行于 1996 年打开了 Chibor 市场、国债发行利率等领域的大门,我国的利率市场化进程也在不断加深。自 2001 年我国成功加入 WTO 组织后,各种各样的利率矛盾问题层出不穷。2008 年的金融危机让世界各国越来越关注极端风险的预测和监管。目前,我国采取了渐进式的利率市场化改革方案,2015 年 10 月 24 日央行彻底放开存款利率管制。随着顺应市场发展趋势的利率调控机制的形成,其服务实体经济的能力也在不断增强。因此,无论是从宏观经济视角还是微观经济视角分析,利率风险度量已成为我国金融风险管理的重要研究课题。(1)从宏观经济视角分析,由于国内的金融总量规模逐步扩大、整体波动性并不平稳,在利率市场上的波动性特点表现为:在 2010 年至 2013 年之间的波动率曲线具有明显的上扬趋势。选择科学有效、准确可行的利率风险度量模型将会直接影响到制定风险管控措施的有效性。目前,随着银行业风险管控自主权的不断扩大,一些矛盾点也随之接踵而来,比如对利率波动的敏感性反应不足、遇到风险时的可控能力较弱等。因此,通过学习国外先进的风险度量方法,加强其自身管控风险的能力,是实现市场平稳、健康发展的首要任务。(2)从微观经济视角分析,我国商业银行对利率风险往往是采用事后管控的模式,对利率波动的实时性反映较为欠缺,随着市场自由化程度的逐步提高,利率波动不断增强,最终会造成存贷利差的大幅缩水,对资本充足率、股东权益等方面产生负面影响,传统的借贷业务也会受到巨大的冲击。
........
1.2 文献综述
1.2.1 国内利率风险度量研究分析
我国利率市场化开始较晚,相关研究与国外有较大差距,但随着市场自由化程度不断加深,使得国内学者对利率风险的分析更加全面、深入。郑文通(1997)首次在国内提出了 VaR 风险度量研究[1]。刘宇飞(1999)提出 VaR模型可以用来评估资产的市场风险,与传统的金融调控方法相比,更能适应复杂的形势[2]。陆蓉等(2000)认为 VaR 方法不仅可以应用于市场风险的管理,同样也适用于对信用风险或其他风险的管理[3]。赵睿等(2002)认为两基金分离定理可以对方差度量进行补充[4]。黄海等(2003)针对 VaR 三种主要计算方法的优缺点进行详细阐述,并着重介绍了 VaR 预测基于参数方法的 EWMA[5]。姚京等(2004)阐述了 Mean-Variance Model和 Mean-VaR Model 的关系[6]。田澎等(2005)认为极端损失的 VaR 值方法,可以更好的解释组合回报的不对称的厚尾现象[7]。杨鹏(2005)提出用压力测试来提高 VaR 模型的准确性[8]。李成等(2007)用 VaR 方法对 GARCH 模型的滞后阶数进行了试算比较,并对 Chibor 数据展开了实证分析[9]。王海侠(2007)认为 VaR 方法为金融监管机构的风险管理及预测提供了有效的工具[10]。冯科等(2009)用 ARMA-GARCH 模型描述同业拆借利率的动态特征,并认为 VaR 方法可以预测其利率风险[11]。陈林奋等(2009)提出在建立 VaR 模型时除了考虑模型的种类,还要考虑分布假设和显著性水平[12]。郭家华(2010)认为在我国银行风险管理领域引入 VaR 方法具有重要的现实意义[13]。朱霞等(2010)认为商业银行应加强对利率风险的识别、度量并分析与信用风险之间的关联性,纳入全面风险管控之中[14]。海威(2010)认为利率市场化后,利率受市场影响波动频繁,用 VaR 模型可以有效监管利率风险[15]。汪寿阳等(2011) 采用 VaR 方法对国际有色金属期货市场风险进行实证分析度量[16]。侯外林(2011)用 ARMA-GARCH 模型估算股指年度收益率的 VaR 值,并对其波动进行了预测[17]。张海波等 (2012)认为 VaR 适用于我国人民币兑美元市场[18]。郭菊娥等(2012)认为物价水平是造成利率期限结构变动的重要因素[19]。辛俚(2012)认为 GARCH 模型对极端风险处理优于混合正态分布模型,但混合正态分布模型对总体的风险度量更为优化[20]。严伟祥等 (2013)基于 GARCH模型来预测对冲基金日交易波动率并估算 VaR 值[21]。何梦泽(2013)基于 GARCH 模型分析得到 Shibor 短期具有波动聚集性,但长期没有体现此特点[22]。房小定等 (2013)认为 GED 分布可以更好地描述 Shibor 对数日收益率序列的分布[23]。黄德权等(2014)以 Shibor 利率的 1W(1 周)和 1M(1 个月)为样本, 建立了基于 ARMA-GARCH 的利率风险 VaR 模型[24]。王田田等(2014)基于 GARCH 模型分析贷款利率管制放开后的 Shibor 的波动特征[25]。张蓉(2014)认为利率波动大多是因为市场预期,并非是现实中的货币存量大小[26]。李艳珍等(2016)基于 GED 分布的 GARCH 模型更精确的拟合利率变动特点[27]。
.......
第 2 章 利率风险度量常用方法
2.1 利率风险形成原因及特点
在世界各国经济关联度逐渐加强的大环境下,金融市场的自由化导致了风险的加剧。而商业银行在金融市场中的核心地位,同时也直接决定了其风险管理能力对各领域的影响力。利率风险是市场风险的重要组成部分。利率风险指的是借贷取得的收益在利率波动情况下与其预期值之间的不对称关系,从而导致借贷价格及交易数量发生变化,造成投资者损失的可能性,其主要形成原因包含市值效应和收入效应。(1)市值效应:商业银行的经济价值随着市场利率的波动而发生变化。但由于商业银行的市值效应不是基于其实时利率及时进行核算,所以其与实际值的变化幅度和方向并不一致。因此,市值效应是风险度量中不可忽视的重要条件。(2)收入效应:利息收入随着市场利率的变化而变化,这一部分是商业银行风险度量的重要内容。针对以非利息收入为主要收入来源的机构或组织,受市场影响较大的此类收入应当计入风险度量的范围之中。利率风险具有损失不确定性、利率变动敏感性和市场利率波动性特点,会直接影响损益的变化。(1)损失不确定性:商业银行的利率风险具有损失性,包括正向的收益和负向的亏损,两者均具有不确定性。损失不确定因素的存在使得商业银行只能单独计算某个概率下的损失大小。(2)利率变动敏感性:商业银行的资产、负债类业务及表外业务对利率波动较为敏感,所以在研究商业银行利率风险因素时,应充分考虑到利率变动敏感性特征。(3)市场利率波动性:利率波动性的存在是利率风险发生的重要条件,如若不存在市场利率的波动性,则利率风险就不会发生,两者是直接因果关系。
........
2.2 商业银行利率风险分类
巴塞尔委员会认为商业银行利率风险不仅会带来负的损失,也可能带来正的利益,但其利率风险是客观存在的。由于利率风险具有损失不确定性、利率变动敏感性和市场利率波动性等特点,使得实际收益波动幅度较大,与预期值负向偏差较大,从而造成一定的风险损失。根据风险来源划分,主要分为 4 种类型。
2.2.1 基差风险(Basic Risk)
Basic Risk 被看作是一种常见的名义利率风险,是由借贷利率的变化幅度和偏向不同,使得净利息收入变化而导致的。它有两种主要表现方式导致净利息收入的减少:一种是存贷利差在时间上的变化幅度不同,导致了资产负债结构的不匹配;另一种是存贷款利率变化幅度不同,导致了存贷利差的缩小。Repricing Risk 是指将在浮动利率条件下的重新定价时间段,与在固定利率条件下的银行表外业务或资产负债业务的到期时间段相比较,得到的两个时间段的差值。由于存在收入效应和市值效应,在利率变动的条件下,当资金借入时定价,其原始成本发生了变化;当资金贷出时定价,其借贷收入发生了变化。两者之间的时间段差值会导致利差的损益,将这种情况下的损益定义为 Repricing Risk。
..........
第 3 章 VaR 方法 ....... 13
3.1 参数选择及计算方法......... 13
3.2 VaR 模型度量方法........... 14
3.2.1 蒙特卡洛模拟法与历史模拟法 ....... 14
3.2.2 方差-协方差法 .......... 15
3.3 VaR 模型检验..... 16
3.4 VaR 模型在风险度量中的优势与弊端..... 17
3.4.1 VaR 方法的优势 ......... 17
3.4.2 VaR 方法的弊端 ......... 18
3.5 小结 ............. 18
第 4 章 Shibor 数据建模及实证研究 ........... 19
4.1 数据............. 19#p#分页标题#e#
4.2 Shibor 利率的基本特征 ....... 20
4.3 常见的 GARCH 族模型....... 28
4.4 GARCH 族模型建模 ......... 30
4.5 引入虚拟变量后的分段 GARCH 族模型分析 ......... 37
4.6 小结............. 44
第 5 章 结论及政策建议 ........... 46
5.1 结论 ............. 46
5.2 政策建议......... 47
第 4 章 Shibor 数据建模及实证研究
利率市场化进程的加快对银行业来说既带来了机会,同时又面临着一些难题。一方面利率波动加剧,对利率风险的度量和监管的要求更为严格;另一方面随着利率市场的逐步完善,对推动银行业转型和服务实体经济的作用越来越显著。本文选用市场化程度较高的 Shibor 数据,用 VaR 方法建立 GARCH 族模型进行实证分析。Eviews 8.0 及 Excel2010 是本文建模研究方面所使用的计量工具。
4.1 数据
当前,全国银行间债券回购利率、Chibor 利率(全国银行间同业拆借利率)、Shibor利率(上海银行间同业拆放利率)具有相对较高的市场化程度。在利率指标及数据特征等方面,综合考量了 Shibor 利率与 Chibor 利率的优劣势,主要从以下几个角度进行对比:(1)数据完整、易获取,具有权威性、可度量等基础特征;(2)利率指标的波动率敏感性、交易规模、市场化程度、科学性等评价维度。在此基础上,最终选择了 Shibor数据作为本文的实证研究基础数据,通过对基础数据在时间和产品种类上的筛选,对其进行对数化的一阶差分步骤,作为本文的实证基础数据。Shibor 是一种单利、无担保、批发性的利率类型,其包括隔夜(O/N)、1 周(1W)、1个月(1M)、3 个月(3M)等。Shibor 与其他基准利率相比较,优势在于:(1)市场典型性,即 Shibor 无论从交易规模、期限周期性和完整性等方面在市场上拥有典型性代表;(2)定价基准性,Shibor 的变动可以引起其他利率的联动效应;(3)波动合理性,Shibor 虽然可以及时反映资金供求关系,但对市场的剧烈波动不会做极端调整,它会保持市场利率稳定在均值附近;(4)政策可控性,央行可通过对 Shibor 的调整,以达到政策意愿水平;(5)经济关联性,Shibor 与其他主要的经济变量维持着显著的关联性关系。本文实证研究数据选取 Shibor,其数据时间选取是从 2007 年 4 月到 2017 年 4 月,其中包含了 121 个月的 Shibor 数据。由于 Shibor 早期数据具有较大的波动性,因此需要剔除其波动性较强的过渡期数据,以便可以准确反映 Shibor 数据的统计特征,并进行有效风险预测。此外,在 Shibor 的各个品种数据中,O/N 利率具有显著的波动性特征,且在利率市场中其交易量也较多,所以最终选取 Shibor O/N 利率为本文的样本数据,样本总容量为 2519。
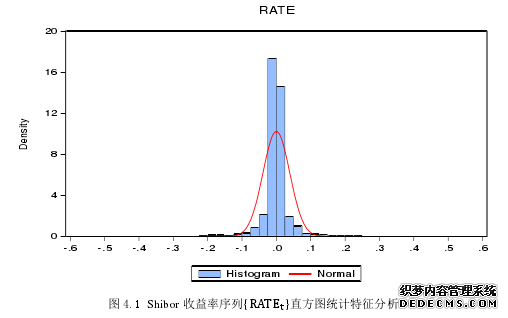

.......
结论
经过对几种常用风险度量方法的优缺点综合分析对比后,最终选择 VaR 方法作为本文的方法论指导。建立 GARCH 族模型以及引入虚拟变量 后的分段 GARCH族模型,对 Shibor 收益率序列{ }分别建立均值方程和条件方差方程,对计算出的VaR 预测值进行准确性检验。通过以上的实证研究分析,可以得出以下相关结论:
(1)由于{ }序列已通过了自相关检验,根据该检验结果可选用 AR(p)模型对样本数据设置均值方程,条件方差方程的设置优先选用GARCH族模型。通过对比AR(1)、AR(2)、AR(3)三种模型的参数显著性检验结果,只有 AR(1)通过了该检验,因此最终选取 AR(1)为该序列的均值方程。在不同模型类型(GARCH、TGARCH、EGARCH)、不同阶数参数{1,2}及不同假设分布(Normal、T、GED)条件下,建立了 36 个 GARCH族模型,通过对这 36 个 GARCH 族模型的 ARCH 效应检验、参数显著性检验及 SC、AIC 值的对比,最终选择 AR(1)-GARCH(2,1)-N 模型、AR(1)-GARCH(1,1)-G 模型、AR(1)-TGARCH(1,1)-N 模型、AR(1)-TGARCH(1,2)-G 模型、AR(1)-EGARCH(1,2)-N 模型这 5 种模型类型,对上述模型计算出的 VaR 预测值进行 Kupiec 回测检验。当置信水平 为 99% 时 , AR(1)-GARCH(1,1)-G 模 型 、 AR(1)-TGARCH(1,1)-N 模 型 及AR(1)-TGARCH(1,2)-G 模 型 这 3 种 模 型 全 部 通 过 了 Kupiec 回 测 检 验 , 但AR(1)-GARCH(2,1)-N 模型、AR(1)-EGARCH(1,2)-N 模型并没有通过 Kupiec 回测检验,造成这种情况的原因可能与模型本身的样本敏感性特征有关;当置信水平为 95%时,5种模型类型全部通过了 Kupiec 回测检验。
(2)基于对 Shibor 收益率序列{ }的残差分布特征分析,发现样本序列呈现出较为显著的阶段性波动特点,采用阶段试探法,引入虚拟变量 对该序列进行分阶段描述,对每个阶段的波动性检验其参数显著性水平。最终选择分段后 AR(1)模型中的 EGARCH(1,2)-N、TGARCH(1,2)-G、 GARCH(1,1)-G 对样本外数据建立模型,计算 VaR 预测值并展开 Kupiec 回测检验。在相同置信水平前提下,分段后 GARCH 族模型的 VaR 预测失败率大幅度降低,模型准确性有较为明显的提高。因此,可以得出最终结论:针对具有阶段性波动特征的样本数据,可以优先选取引入虚拟变量的分段后的GARCH 族模型,该模型可以有效弥补其受样本类型、容量等因素较为敏感的不足,进而可以提高 VaR 预测风险的准确度。
..........
参考文献(略)

