本文是经济论文,自Box和Jenkins(1970)系统地阐述了ARMA模型的识别、估计、检验及预测的原理和方法以来,模型的理论和应用方面得到了极大的发展,而在模型参数估计方面仍以LS估计和LAD估计为主。可是随着这研究的深入,我们发现在金融领域中数据往往带有异常点并且具有重尾性质,此时LS估计就显得不够稳健而LAD估计又无法消除异常点的影响。有鉴于此,本文考虑能否使用SM-估计得到更为稳健的参数。本文的研究内容和成果总结如下:(1)阐述了ARMA模型的研究内容及其实际应用,并梳理了从LS估计、LAD估计到SM-估计的发展过程。结合重尾ARMA模型与SM-估计的思想,提出了重尾ARMA模型的SM-估计.(2)从同方差性和异方差的重尾ARMA模型两种情况出发,在无需假设残差方差存在的前提下,证明了SM-估计的相合性和渐近正态性。(3)在残差服从不同重尾分布的情况下,对SM-估计、LAD估计和LS估计的估计效果进行数据模拟.通过数据模拟结果比较得知,无论残差方差是否存在、模是否具有异方差性,SM-估计的效果是最好的。(4)实证选取深证成指真实数据,在使用SM-估计、LAD估计以及LS估计得到的四个ARMA模型的基础上加入使用GARCH模型并进行对比,发现SM-估计的效果最好,与数据模拟结论一致。
.......
第1章绪论
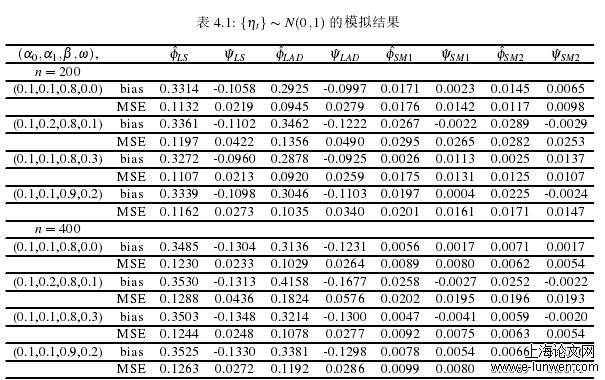
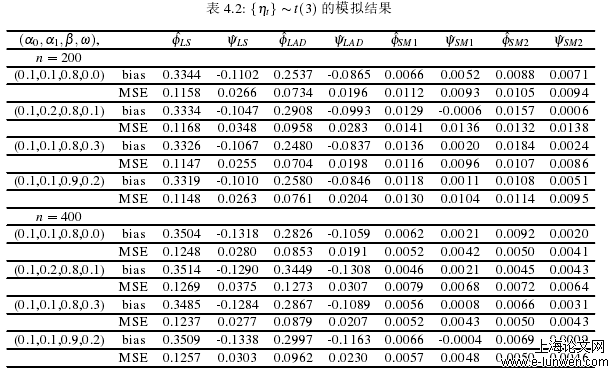
本文创新点如下:1.针对LS估计和LAD估计的不足,本文对重尾ARMA模型提出SM-估计方法,即通过对重尾数据中的异常点赋予相对而言更低的权重,以此来使整体的误差达到最小,使它的估计结果更稳健。2.对SM-估计的理论性质进行了研究,即在一定假设条件下,证明了在同方差和异方差两种情况下的重尾ARMA模型参数估计中的相合性和渐近正态性,并在误差方差有限和方差无限的情况下分别进行蒙特卡洛模拟。从模拟的结果中发现,SM-估计的bias和MSE都是最小的,其结果明显优于LS估计和LAD估计.3.将SM-估计运用到深证成指的实际数据中,根据日收盘价的对数收益率建立ARMA模型,并针对残差序列进行异方差检验进而建立ARMA-GARCH模型.从估计结果的MSE和MAE来看,SM-估计的效果要好于LS估计和LAD估计。众所周知,对于ARMA模型的参数估计,目前运用最多的是ML估计和LS估计。对于ML估计和LS估计,只有在假设模型的误差方差存在的条件下,才能得到较好的估计效果。但是金融数据通常具有重尾性质,这些数据的方差可能是无穷的,此时使用ML估计和LS估计就显得不够稳健。
.......
第2章理论背景
2.1ARMA模型
在时间序列中,某个因素的改变都会引起序列值发生变化,但是从时间序列整体来看,变化又是有规律可循的,我们可以利用历史数据发现其中的规律和相关关系,从而建立起一个相应的数学模型来拟合这个时间序列,刻画它内在的规律,最后利用该模型预测未来的走势。为了应对这个问题,Box和Jenkins(1970)提出了ARMA模型,它是目前最常用的拟合平稳时间序列的模型,在金融领域上具有重要意义。在此,我们简要介绍ARMA模型的定义、识别定阶、建模步骤等内容。于是,学者们提出使用最小一乘(LAD)或者M-估计去替代ML估计和LS估计,其中LAD估计是M-估计的特殊形式。尽管与ML估计和LS估计相比,M-估计无需假设误差方差存在并且具有较强的稳健性,但是它本质上给予异常点和正常点相同的权重,无法有效减少极端值以及高杠杆点的影响,以至于某些情况下无法保证渐近正态性的存在。
2.2参数估计方法
我们建立的模型中往往存在着未知参数,只有运用适当的参数估计方法得到准确的参数,才能获得接近真实的模型。本节,我们简要介绍LS估计、M-估计、SM-估计以及它们之间的关系。有效的LS估计往往需要满足同方差、正态性、单一模型的假设。然而,现实中的数据往往不满足这些条件。比如金融时间数据呈现重尾、异方差性质,此时的LS估计稳健性很差,估计的参数并不理想。
.......
第3章重尾同方差ARMA模型的SM-估计...........................10
3.1引言........................................10
3.2SM-估计的渐近性质...............................10
3.3定理明.....................................13
3.4数据模拟.....................................31
第4章重尾异方差ARMA模型的SM-估计...........................34
4.1引言........................................34
4.2SM-估计的渐近性质...............................35
4.3定理证明.....................................36
4.4数据模拟.....................................42
4.5实证分析.....................................44
第5章总结与展望..........................................49
........
第4章重尾异方差ARMA模型的SM-估计
4.1引言
根据上述结论,我们在ARMA(2,1)模型描述收益率的基础上加入结构简洁并且拟合重尾残差效果较好的基于t分布的GARCH(1,1)模型来拟合误差,GARCH(1,1)模型的参数由极大似然估计方法得到。最后,在初始值已知的情况下,我们使用ARMA(2,1)-GARCH(1,1)模型得到800个模拟数据,并与原数据进行比较,得到均方误差(MSE)和平均绝对误差(MAE)在上一章我们研究了残差{εt}为独立同分布序列的重尾ARMA模型的SM-估计,但在金融领域,拟合后的残差项常常呈现条件异方差性质。因此本章重点研究重尾异方差ARMA的SM-估计方法,并证明该估计的相合性和渐近正态性。在上一章我们研究了残差{εt}为独立同分布序列的重尾ARMA模型的SM-估计,但在金融领域,拟合后的残差项常常呈现条件异方差性质。因此本章重点研究重尾异方差ARMA的SM-估计方法,并证明该估计的相合性和渐近正态性。

4.2SM-估计的渐近性质
通过第三章以及本章的理论研究和数据模拟,我们有理由相信对于同方差和异方差两种情况下的重尾ARMA模型,SM-估计的估计结果明显比LS估计和LAD估计,所以本节利用R软件,将SM-估计用于实际的深证成指数据中,并将估计的结果和LS估计、LAD估计的结果作比较。本章选取深证成指2016年2月19日至2019年5月31日的收盘价,共计801个数据。令pt为深证成指第t个交易的收盘价,rt=log(pt)−log(pt−1)为日收益率,所以由收盘价pt得到800个日收益率rt数据。日收益率的时间序列图及基本统计情况见图4.1和表4.4.由表4.4可见,在样本区间内深证成指对数收益率的均值、中位数都为负;偏度小于0,说明负的收益率的频数大于正的收益;峰度大于3,说明样本区间内,具有重尾的特点;JB统计量很大且对应的p值趋近于0,故序列不服从正态分布。使用ADF检验方法判断日收益率序列的平稳性。结果显示,DF值为-8.632,p值为0.01,当显著水平为0.05时拒绝原假设,即日收益率序列是平稳的。

........
第5章总结与展望
(1)在证明异方差ARMA模型的SM-估计的相合性和渐近正态性时,本文的假设条件比较严格,适合该证明的模型和方法比较有限。今后可以尝试使用更加宽松的条件证明本文SM-估计的性质。(2)本文在SM-估计的模拟、实证中,只选取SLAD估计和S-Huber估计进行分析。在以后的SM-估计研究中可以尝试其他的ρ(·)函数,如Hampel函数等。在权重的选取上,也可以尝试其他的权重函数,使得SM-估计的效果会更好。(3)在实证研究对象上,本文仅仅考虑了深证成指数据,今后可以将基于SM-估计的重尾ARMA模型延伸到其他金融市场中。
参考文献(略)

