管理论文哪里有?在本论文中,首先对机组组合问题进行概述。提出改进双重粒子群算法和基于算法的含风电、火电的机组组合优化模型。然后,使用不同的优化算法进行求解分析。最后通过算例进行仿真验证,结果证明所提出的算法的正确性。然而,对本文进行的研究仍存在很多的不足之处和下一步深入学习的地方。
第 1 章 绪论
1.2 研究现状与分析
机组组合优化问题是电力系统经济调度的基础,一直是专家、学者研究的重点问题,对机组组合优化的研究是从 20 世纪开始的。伴着中国和世界上的其他国家经济的飞快发展以及城市和乡村居民对电力使用量逐年增多,对机组组合优化问题的研究受到了大家越来越多的关注。
1.2.1 机组组合问题的研究现状
伴着对机组组合优化问题的深入研究,在机组组合优化模型中增加了大量附加约束限制,使机组组合优化模型能够完美地展示火电机组的不同时刻的运行状态情况。在对火电机组组合的研究过程中,因为机组组合优化问题呈现出高维度、非凸性、非线性、离散等一系列多种不同的问题。因此,在求解的进程中,求解出最理想的解是相当复杂的,机组组合优化的研究一方面可以带来巨额的经济成本,另一方面也可以治理一系列环境污染问题,所以一直都是电力系统范围内的研究热点[8][9]。
对机组组合优化问题求解的算法包含两大部分:第一部分是传统的优化算法,第二部分为智能优化算法。
1.传统的优化算法
(1)优先顺序法
优先顺序法:在求解的进程中,占计算机内部的存储空间十分小、求解的速度呈现秒级。在求解机组组合优化进程中,其结果可能找不到最优解,但是一定会寻找到一个最符合初始条件的解,目的是时刻都能够满足火电机组在某时间段的运行状况[10]。缺点:其算法不能满足在求解时受到某些特殊限制因素。如:对火电机组的优化、大面积的水电机组的优化。在一定的时间范围内,解决这种大面积的耦合难题时找到最优解是十分困难的。
文献[11]提出一种特殊的优先顺序法来求解机组组合问题。在分析优先顺序方法特性的基础上,按照一定的经济指标,分析机组的出力在不同区间内,在不同的邻域内可以构成不同的机组组合结果,最后由机组的不同排列次序重新定义机组的优化。

第 3 章 基于改进双重粒子群的机组组合优化研究
3.1 基于改进双重粒子群的机组组合优化总体框架
机组组合优化问题,是电力系统调度优化讨论的根源,对机组组合优化的分析一方面可以带给人们巨额的经济利润,另一方面也可以给社会带来超额价值。所以,它总是中国和世界上其他国家的电力系统的专家和学者研究的中心。机组组合优化问题,指在特定的某个时间范围内,在保证机组无故障工作的条件下,如何分配某些机组的启停和功率的使用状况,以满足发电成本费用最低[48]。机组组合优化问题常常分为两个方面:第一个方面计划每台机组的启停[49],第二个方面是明确每台机组的发电功率[50],目的是确保用电的供应和需求是一样的,这两个途径相互依靠、相互存在。机组组合优化问题在求解的步骤中需要加入大量的约束限制,其构建的模型是一个大范围的耦合难题。
为了使火电机组的煤耗成本达到最小。为进一步充分地分析火电机组组合优化调度情况,本章提出改进双重粒子群算法的机组组合优化模型,改进双重粒子群算法分为两个部分,第一个部分用离散粒子群算法(DPSO)优化机组的开停机;第二个部分是用快速粒子群算法(APSO)优化每台机组的功率分配情况。对每台机组的爬坡速率约束限制,利用罚函数来代替,这样做的目的是保证机组的功率分配保持一致。
第 4 章 基于广义 Benders 算法的含风电的机组组合优化
4.1 Benders 算法和广义 Benders 算法
为了平衡所有机组在运行条件限制的状况下,机组组合(unit commitment,UC),能合理规划在第二日的某个时间段内火电机组的启动、停机状况。然后分别对各个不同时段的火电机组出力的情况进行分配,最后使整个系统总的运行费用达到最小值[58]。在经济调度中,机组可以进一步达到对发电自动调节、对电压自动调节[59]。
风电具有随机性、间歇性特点,大范围的风电加入电网中,早期的机组组合优化手段不能适应新型能源系统中的所有问题。对于含风电的机组组合,由于风电引起的功率不稳定,为了保证电力系统平稳运行、达到经济性最优,机组组合优化算法具有十分关键作用。传统算法在求解含风电的机组组合优化时,求解速度特别慢。因此,在对大型的电力系统进行调度时,在可以承受的不同时间范围内,得到一个可行的、误差范围很小的解是相当困难的。目前的传统优化方法有:优先级表法[60]、动态规划法[61]、拉格朗日松弛法[62]、混合整数规划法[63]。还有,人工智能方法:如模拟退火算法[64]、蚁群算法[65]、遗传算法[66]、粒子群算法[67]等。对于所列出的算法进行求解,最后可以获得很多满意的结果。但是它们的计算的速度十分缓慢,求解的精确程度上还有待进一步的提高。
含风电的机组组合具有维数高、非凸、呈现离散型、非线性的特点。这种对复杂的问题进行求解分析时,使用的大多数的情况下是广义 Benders 分解算法方法,在求解范围比较大的混合整数规划问题时,通常将原问题分解若干上、下层规模相对较小的问题,经过多次循环求解,最后可以获得与原问题一样的结果。本文所提的分解算法完全能够对变换后的问题进行求解,并可以得到理想的解集,最后可以满足求解范围比较大的、非线性的、混合整数规划的要求。
4.2 基于广义 Benders 算法求解含风电的机组组合
4.2.1 含风电的机组组合模型建立
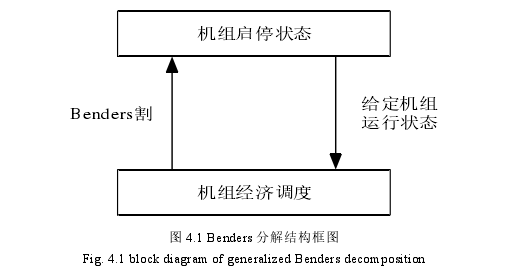
在广义 Benders 分解算法中,它主要的方法是分层优化处理、循环迭代求解分析。所以,本文使用广义 Benders 分解算法求解分析时,它主要的方法是:第一部是将来的原问题划分解为以机组运行状态的机组组合状态的确定的子问题,另一子问题是以系统出力的系统经济调度问题。对分解后的这两个子问题分别进行相互之间的迭代求解分析。最后可以得出最佳的答案。
首先,对火电机组运行状态进行分别设定。其次,机组组合问题就转变成为经济分配的问题。通过对这个问题进行求解分析时,一方面可以获得机组出力的详细的数目,另外一个方面也可以得获机组的经济总成本的数据。它们之间以Benders 割的形式返回到机组上层运行状态的子问题中,然后就可以开始再一次的机组的开机、关机状态的迭代循环操作。其中整个过程可以图 4.1 表示。
第 5 章 总结与展望
5.2 展望
在本论文中,首先对机组组合问题进行概述。提出改进双重粒子群算法和基于算法的含风电、火电的机组组合优化模型。然后,使用不同的优化算法进行求解分析。最后通过算例进行仿真验证,结果证明所提出的算法的正确性。然而,对本文进行的研究仍存在很多的不足之处和下一步深入学习的地方。未来需要进一步学习和论讨的地方有 3 点:
在风火机组组合优化中,风电出力随机性,考虑机组功率出力的分配使用情况的时候,单一只考虑风电的随机性这一因素。考虑到风电场出力特性的多方面的特点,从而可以充分应用风力发电的这两个特性。
提高优化算法的求解分析时的高效的特点。虽然本文提出的广义 Benders分解算法、改进的粒子群优化算法。它们都在一定的范围程度内提高了优化算法的效率值。但是,在整体来看来算法的效率值仍然可以有进一步的提升,算法的求解速度还有提升的空间。
对含风电机组组合优化模型补充。在目前的情形中,通过构建含风电机组组合优化的模型,不仅仅需要更加深入补充与大量的限制条件,也达到更好的研究机组的运行情况。
参考文献(略)

