本文是一篇工程论文,工程论文只能有一个主题(不能是几块工作拼凑在一起),这个主题要具体到问题的基层(即此问题基本再也无法向更低的层次细分为子问题),而不是问题所属的领域,更不是问题所在的学科,换言之,研究的主题切忌过大。(以上内容来自百度百科)今天为大家推荐一篇工程论文,供大家参考。
第一章 绪论
1.1 研究背景与意义
为保证电力系统在日常生产过程中最大限度地满足经济、环保、安全、可靠的需求,“源-网-荷”每个环节中将遇到各类优化问题,包括调度计划优化[1,2]、控制器参数优化[3,4]、检修计划优化[5]等问题。这些优化问题都是在满足不同运行安全约束的条件下,来追求运行人员所需要达到的目标。因此,目标函数及约束条件的形态和规模就决定了优化问题的求解难度和优化算法的选择。对于各类优化问题,最常用的求解方法可分为经典数学方法和人工智能算法两大类[6]。一般来说,基于梯度的经典数学方法具有求解速度快、收敛性可靠等优势,例如牛顿法[7]、线性规划[8]、二次规划[9]、内点法[10],然而当系统存在较强的非线性、不连续的目标函数以及约束条件、离散变量、以及多个极值最优解等特征时,这类方法寻优性能就难以满足要求,容易陷入局部最优[11]。比如最经典的电力系统经济调度问题,当考虑到汽轮机的阀点效应[12]、发电机的禁止运行区域约束[13]、多燃料导致成本函数[14]的分段性等情况时,优化模型就会呈现出不连续、不可导、多极值及多分段约束等特征,此时经典数学方法就难以求解。此外,由著名数学家贝尔曼(R. Bellman)提出的动态规划法则不依赖于具体优化模型的形态[15],可以获得全局最优解,但随优化问题规模的增长,该数学方法容易出现“维数灾难”问题,无法求解。与经典数学方法相比,人工智能算法对优化问题数学形态的依赖性更低,应用灵活性更高。最常用的人工智能算法都是受自然生物生存机制[16]和物理现象[17]启发提出的,其中最著名的算法包括受自然界“适者生存”规则启发的遗传算法(genetic algorithm,GA)[18]和受鸟 群捕食启 发的 粒子群(particle swarm optimization, PSO)[19]。根据NFL(no-free-lunch)[20]理论可知,没有一种算法是可以完美求解所有的优化问题。因此,近些年来还有很多学者提出各类启发式优化算法,在群体智慧的合作体系中实施随机的全局搜索和精确的局部搜索,提高获得全局最优解的概率。这类启发式人工智能算法也容易出现两个弊端[21]:① 寻优随机性较高,即每次获得的最优解可能存在较大差异,需要运行多次筛选出最好的结果作为电力系统优化决策;② 寻优时间较长,难以满足大规模电力系统较短时间尺度的实时优化任务需求。
.........
1.2 国内外研究现状
1.2.1 经典优化方法及其在电力系统优化的应用
如前文所述,经典优化方法包括经典数学方法及启发式人工智能算法。为此,本章节将详细介绍三种常用的优化方法,分别为内点法、遗传算法以及粒子群优化算法,分别如下:(1) 内点法基于单纯形法的结构框架,Karmarkar 于 1984 年提出了一种全新的线性规划方法,该方法从可行域内的某一初始解出发,沿着最速下降方向寻优,在可行域内直接逼近最优解,因此该算法也被称为内点法[24]。随着国内外学者对内点法的不断研究发展,该方法大致可分为三大类,分别为投影尺度法、仿射尺度法和路径跟随法,其中第三种算法具有高收敛可靠性、强鲁棒性以及对求解问题规模敏感性低等优势[25]。因此,内点法及其改进的算法已成功被应用于电力系统的各类优化问题,包括最普遍的最优潮流问题[26]及子优化问题(无功优化和经济调度)[27,28]。(2) 遗传算法GA 作为最常用的启发式人工智能算法,是一种启发于生物进化论及遗传学机理的随机搜索算法[29]。与其他启发式算法一样,该算法对求解问题的数学形态依赖性很低,非常适合求解含多极值、多约束、不连续不可导目标函数的非线性非凸优化问题。此外,GA 具有较高的寻优鲁棒性,容易实现分布式并行计算,因此 GA 已广泛应用于电力系统的不同优化问题。对于含有离散变量的电力系统机组组合问题,文[30]科学地设计了GA 的应用求解过程,仿真结果表明 GA 可以有效地避免陷入局部最优解。同样地,对于含有混合变量的非线性无功优化问题,GA[31]、改进量子遗传算法(quantum-inspiredgenetic algorithm, QGA)[32]、二次变异遗传算法[33]以及改进小生境遗传算法[34]均可以提高收敛最优解的质量,同时可保证较快的寻优速度。
..........
第二章 电力系统的迁移强化学习优化理论框架
2.1 集中式迁移强化学习
集中式迁移强化学习(centralized transfer reinforcement learning, CTRL)是指迁移学习与单智能体强化学习的结合算法,主要用于求解电力系统的集中式优化问题。作为强化学习最广泛应用的算法之一,单智能体 Q 学习可以在智能体与外部环境的不断交互后,根据反馈得到的奖励值,即可更新每个状态下的动作策略知识,如图 2-1 所示。首先对每个源任务的最优知识矩阵及特征信息进行保存,其中特征信息就是区分不同任务之间的主要信息,例如电力系统经济调度优化任务的特征信息是负荷的需求和所有开启机组的可调度区间。当出现新的优化任务时,则可从源任务中的最优知识矩阵提炼出新任务的初始化知识矩阵,其中迁移学习技术的不同也直接决定了提炼过程,为使得初始化的知识矩阵更逼近新任务的最优知识矩阵,就需要设计合适的迁移技术。需要说明的是,初始化知识矩阵的改造也是本文的研究核心之一。传统强化学习往往只采用单个智能体在未知环境中探索,因此算法每次只能更新知识矩阵中对应的一个状态-动作知识。为此,迁移强化学习可利用群智能技术[99]来实现高效的探索(例如蜂群中侦查蜂和采蜜蜂的分工合作、蚁群中个体信息素的共同作用),不仅在每个状态下可以实施多个动作选择,而且可以比较每个动作选择的奖励值,从而使得知识矩阵的更新更为高效。另外,当存在源任务与新任务非常相似的情况,即可将源任务中的部分探索样本迁移到新任务中,从而加快学习效率。
..........
2.2 分散式迁移强化学习
与 CTRL 一样,分散式迁移强化学习(decentralized transfer reinforcement learning,DTRL)采用相同的知识存储方式、知识矩阵迁移技术、群智能探索学习。两者最大的不同是:DTRL 采用的核心算法是多智能体强化技术,用于求解电力系统的集中式优化问题。目前,绝大多数多智能体强化学习的底层算法均采用经典 Q 学习,也符合本文采用Q 学习的智能体学习模式。对于不同的分散式优化问题,根据智能体之间的合作/竞争关系,就可以选择合适的多智能体强化学习技术来求解,如图 2-2 所示。为较好构造智能体之间的合作/竞争关系,本文采用一致性协同理论[102]与博弈论[103]分别来实现智能体之间的互动协调,从而找到多智能体之间的最优均衡解。分散控制系统的基本问题之一是使所有智能体达到一致性。在一个多智能体网络中,当所有智能体与相邻智能体之间通过信息交流,对所关心的变量取值达到共识时,就称它们达到一致[104]。因此,本文利用协同一致性算法来实现不同智能体之间的知识交互,使他们的追求达到一致,即最大化整个多智能体系统的利益之和。
........
第三章 连续单任务迁移强化学习算法及应用......16
3.1 连续单任务迁移强化学习原理.........16
3.1.1 知识存储与学习............16
3.1.2 探索与利用..........17
3.1.3 连续单任务知识迁移....19
3.2 电力系统无功优化应用...........20
3.2.1 无功优化模型......20
3.2.2 算法求解设计......21
3.2.3 算例仿真....24
3.4 本章小结.....34
第四章 多任务线性迁移强化学习算法及应用......35
4.1 多任务线性迁移强化学习原理.........35
4.2 含风光车的 AGC 功率动态分配应用 ........39
4.3 虚拟发电部落的 AGC 功率动态分配应用 ..........51
4.4 本章小结.....69
第五章 多任务非线性迁移强化学习算法及应用............70
5.1 多任务非线性迁移强化学习原理.....70
5.2 电力系统分散式最优碳能复合流应用.......77
5.3 电力系统供需互动实时调度应用.....96
5.4 本章小结............. 111
第五章 多任务非线性迁移强化学习算法及应用
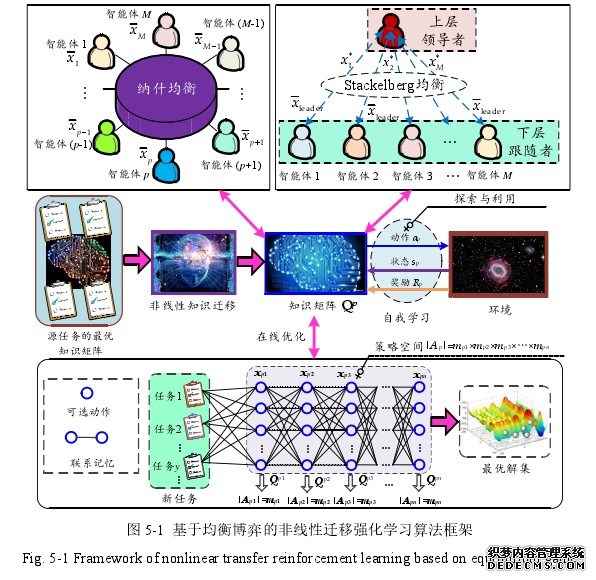
5.1 多任务非线性迁移强化学习原理
5.1.1 多智能体均衡博弈机制
#p#分页标题#e#
上一章采用的多智能体协同一致性机制,本质上来讲,智能体之间是属于完全合作关系的,然而,大规模电力系统的“源-网-荷”不同区域往往归属不同的利益主体公司,因此,智能体之间往往无法达到完全合作的程度,更多的是在满足整个系统运行安全的前提下,进一步追求自身的利益最大化。因此,本章引入了更加符合实际智能体关系的博弈机制。上一章仿真也分析到在智能体数量较多的情况下,基于知识矩阵的博弈均衡点容易出现计算困难,无法求解。为此,本文将利用变化的适应度函数来不断逼近均衡点[133],该机制更加简便、计算更加快速。Stackelberg 均衡博弈[153]作为一种典型的分层博弈,其本质上也是一种竞争博弈策略。纳什均衡博弈中智能体是对等的,动作决策都是公平对等的,与之不同,Stackelberg均衡博弈对智能体进行了角色划分,包括领导者和跟随者,其中领导者占据更多的主动权。一般领导者在上层先制定出自己的策略,然后下层的跟随者再根据领导者的策略再作出自己的最优决策,再将其最优决策反馈到上层领导者,为领导者提供下一轮的决策依据,这样不断交互博弈之后,智能体之间就可以形成一个最优的联合动作策略.

.......
总结
总的来说,本文首次提出了一类全新的迁移强化学习优化算法,并应用到电力系统的不同优化问题,主要贡献可总结如下:
(1)首次提出了电力系统的迁移强化学习优化理论框架,根据迁移方式以及智能体优化框架的不同,划分了不同的迁移强化学习分支,用于解决电力系统的不同优化问题。
(2)设计了连续单任务迁移强化学习的单智能体基础算法,包括:① 利用经典 Q 学习构造智能体的学习模式,并提出联系记忆的方式实现知识矩阵的高效存储,有效解决大规模复杂电力系统高维变量导致的“维数灾难”;② 采用多主体协同的学习方式,可明显提高知识矩阵的更新效率;③ 基于群智能技术的探索与利用,可有效平衡算法全局搜索与局部搜索的比重,有效提高算法收敛最优解的质量,避免陷入低质量的局部最优解;④ 将相邻历史任务的最优知识矩阵迁移到新任务的初始知识矩阵,避免了各个主体在新环境中的盲目搜索,可明显提升算法的收敛速度;⑤ IEEE 300 节点算例下,所提算法计算速度可达 ACS 算法的 100 倍以上。
(3)提出了两种不同的多任务线性迁移强化学习算法,包括:① 引入二进制知识和模仿学习的 IQ 算法,有效解决了连续控制变量的优化及知识储存问题,同时加速了算法在知识初始形成阶段的探索与利用过程,海南电网的集中式 AGC 功率动态分配仿真模型表明:广域虚拟发电厂可以有效地管控风光车参与 AGC 控制,提高区域电网的动态响应速度,IQ 算法可以在较短时间内获得不同总功率指令下的高质量最优解,明显提升了 AGC 控制性能指标,降低系统总的调节本;② 利用一致性协同理论将单智能体迁移强化学习扩展为具有多任务线性知识迁移的多智能体 CTQ 算法,可以有效解决完全合作式的分散式优化问题,基于总功率指令偏差的任务相关性评估可以有效实现AGC功率动态分配的多任务线性知识迁移,虚拟发电部落的概念框架有效实现了 AGC 功率动态分配的分层分散优化,广东电网实际算例表明:在引入多任务知识迁移后,CTQ 算法能有效加速收敛速度,满足 AGC 功率动态分配的在线优化需求,同时,算法可以收敛至高质量的最优解,不同季节下的随机负荷扰动控制性能指标均优于其他现有算法。
..........
参考文献(略)

