1 绪 论
1.1 全局影响分析的研究概况
数据删除法在统计模型的影响分析研究中是一种比较完善的分析方法。早在1977 年,著名统计学家 Cook 就基于置信椭球提出了这种方法,以判断各个数据点对满秩线性回归模型的最小二乘估计的贡献。此种方法的特点是通过对比完全删除某个观察值前后估计量的变化程度来度量相应观察值的影响程度,如果当删除某个观测点后,分析的重要特性发生了大幅的改变,则认为该观测点是强影响点。随后,Cook (1979)、 Beckman 和 Cook (1983) 、Chatterjee 和 Hadi(1986)等人不断地完善了这种方法,给出了判别异常点、高杠杆点和影响点的若干统计量。人们还将此种方法推广到其它统计模型中去,如 Pregibon(1981)将其推广到 logistic 回归模型,Williams(1987)将其推广到广义线性模型等。目前已有基于残差、似然函数等的多种尺度,并针对每种尺度提出了若干统计量,如就探测影响点而言较为常见的统计量是 Cook 距离统计量、Welsch-Kuh 统计量、协方差比统计量等。这种方法研究的比较早,所以理论及应用比较成熟,目前已有大量的专著问世,详见Belsley,Kuh 和 Welsch(1980)、Cook 和 Weisberg(1982)、Chatterjee 和 Hadi(1988)、韦博成(1992)等。近年来,人们更多地关注的是多个影响点的探测,如 Imon(2005)和 Nurunnabi 等(2010)分别研究了线性模型和广义线性模型中判别多个影响点的方法、Nurunnabi 等(2011)利用 Pena(2005)处理单个影响点的方法进一步研究线性模型中判别多个影响点的方法。尽管数据删除法直观,易于理解,便于统计上的处理,同时适用性广,可以用于各种统计模型的影响分析,然而数据删除法也有其缺点,它往往很难探测影响点之间的掩盖和提升作用。
………..
1.2 局部影响分析的研究概况
统计学家 Cook 在 1986 年从微分几何观点分析似然距离的变化,利用似然距离的影响图的法曲率来研究扰动的局部影响,提出了局部影响分析法。该方法突出的特点是通过给观测值一个微小的扰动,而不是完全的删除,然后对比扰动前后估计量的变化来度量观察值的影响程度。该方法可以同时扰动所有数据点,因此可以判断多个影响点,从而可以比数据删除方法更容易评估数据的联合扰动带来的影响。这从一定程度上克服了影响点之间的掩盖与提升效应。此外,该方法还可用于考虑模型有微小扰动时对统计推断的影响。正是因为有着诸多的优点,该方法近年来得到了广泛的研究与发展,并被推广到若干其它统计模型。比如,Bechman 等(1987)研究了混合模型方差分析的局部影响分析;Lawrance(1988)研究了 Box-Cox 变换模型的回归系数的局部影响分析;Thomas 和 Cook(1989,1990)把局部影响的方法推广到了广义线性模型;Weissfeld(1990)研究了比例风险模型的局部影响分析;Escobar 和 Meeker(1992)研究了带删失数据回归分析的局部影响分析;St.Laurent 和 Cook(1993)研究了非线性模型的局部影响分析,并分析了杠杆、局部影响以及曲率之间的联系;Zhao 和 Lee (1995)、Lee 和 Zhao(1996)研究了测量误差模型的局部影响分析;Farrell 和 Cadigan (2000)研究了二项回归模型的局部影响分析;Lee 和 Wang(1996)及 Poon 等(1999)研究了结构方程模型的局部影响分析;Lesaffre 和 Verbeke (1998)研究了线性混合模型的局部影响分析;Galea 等(1997)和Liu(2000)研究了椭球线性模型的局部影响分析;Zhu 和 Li(2001)提出了基于 Q 函数的统计诊断方法,其主要想法是用 EM 算法中的 Q 函数取代对数似然函数来构建 Cook 统计量,解决了不完全数据模型的影响分析;Zhu 和 Lee(2003)研究了广义线性混合模型的局部影响分析,他们把随机效应处理成缺失数据,然后用其提出的不完全数据下的局部影响分析法得到了此模型六种扰动模式下的影响点的探测;Shi(2009)等讨论了具有缺失数据的广义线性模型的局部影响分析;Villegas 等(2013)研究了广义对称线性模型的局部影响分析等。
………
2 局部影响分析的基本理论与方法
2.1 数据删除方法与 Cook 距离
在局部影响分析的研究中学者们还注意到如下两个问题。第一个问题是如何扰动模型,该问题之所以重要是由于随意的选择扰动模式可能导致不恰当的统计推断。在相对简单的模型中,扰动方式的选择是比较自然的,如经典的线性模型中选择对样本点加权就是一种很自然的扰动模式。然而当模型比较复杂时,往往很难直观的选择自然的扰动模式。第二个问题是如何在目标函数具有非零一阶导数的点上建立影响测度,Fung 和 Kwan(1997)注意到在局部影响分析中,当目标函数由似然距离改为参数估计或检验统计量时,在这些目标函数的一阶导数不为零的点处,法曲率不是伸缩不变的,因此可能得到模糊的诊断结果。同样可以说明,Poon 和 Poon(1999)提出的共形法曲率也不是尺度不变的。这会导致在判断法曲率大小上缺乏客观的评价标准,并影响局部分析方法的应用。针对这两个问题,Zhu等(2007)提出了一个基于似然函数的、普适性很强的关于扰动模式的选择和相应的局部影响评价的方法。该方法是通过引入扰动流形(pertubation manifold)和度量张量(metric tensor)的概念进行扰动选择和影响评价,并可以应用于任意目标函数任意点处的影响分析。总而言之,Cook 局部影响分析是一种基于似然函数的统计诊断方法,用于评价既定模型和数据的微小扰动对统计推断的局部影响。目前,局部影响分析方法已成为统计诊断的一种重要方法,在诸多方面有广泛应用。
………
2.2 影响图概念
通对对模型引入适当的附加条件也是解决变量之间存在复共线性的一种有效方法。附加条件常以等式约束、不等式约束、随机约束、椭球约束等形式表现,所以对约束下的模型进行影响分析研究是有必要的。近年已有不少学者开始了这方面的研究,如 Paula(1993)研究了不等式约束下线性模型的局部影响分析、Paula(1995)研究了约束广义线性模型的全局影响分析、Gu 和 Fung(2001)研究了等式约束的局部影响分析、Liu 等(2009)研究了随机等式约束的局部影响分析、Paula和 Cysneiros(2010)研究了广义线性模型下带线性等式约束和不等式约束的局部影响分析,他们利用二次罚函数来替代对数似然函数从而得到了带约束的影响曲率。虽然有偏估计和受约束模型的影响分析已有不少结果,但这方面的研究工作还不完善,还有大量的工作要做。
…………
3 基于线性模型的影响分析研究 .........17
3.1 线性模型参数估计的发展概述 ..... 17
3.2 统一有偏估计的残差分析 ....... 18
3.2.1 问题的提出 ........ 18
3.2.2 统一有偏残差 .... 19
3.2.3 几乎无偏统一有偏残差 ...... 22
3.2.4 数值算例 ...... 23
3.3 线性模型两参数估计的局部影响分析 ..... 26
3.4 带随机约束线性模型的岭估计的局部影响分析 ....... 33
3.5 本章小结 ..... 44
4 等式约束下椭球线性模型的局部影响分析....... 45
4.1 引言....... 45
4.2 模型与估计....... 45
4.3 局部影响分析......... 48
4.3.1 方差的扰动 ........ 49
4.3.2 因变量的扰动 .... 50
4.3.3 设计矩阵的扰动 ...... 50
4.4 数值算例..... 51
4.5 本章小结..... 56
5 广义线性模型岭估计的局部影响分析 ..... 57
5.1 引言....... 57
5.2 模型与估计....... 58
5.3 局部影响分析......... 60
5.4 数值算例..... 63
5.5 本章小结..... 65
6 等式约束下广义对称线性模型的局部影响分析
6.1 引言
众所周知,正态线性模型具有广泛的应用,为连续对称数据建模提供了重要的统计工具。然而,当对称数据较之正态分布呈现厚尾或者轻尾时,一些极端观测数据可能对极大似然估计造成严重的影响。为了减低这样的影响,则引入了对称线性模型作为正态线性模型的推广,以处理一些具有厚尾或者轻尾的真实数据的统计建模问题。在对称线性模型中,因变量服从对称分布,其期望(如果存在的话)与线性预测(linear predictor)之间的关系为恒等关系。由于其重要性,对称分布族近年来受到了广泛的关注,并被应用到多个应用领域中,它包含了一大类具有重要的实际意义的分布,比如学生氏t分布、幂指数分布、双曲分布等,其详细讨论与应用可以参见 Fang 等(1990)、Fang 和 Anderson(1990)。而对称线性模型影响诊断方面的研究可以参见 Galea 等(2003)、Cysneiros 和 Paula(2005)。广义对称线性模型则是基于对称线性模型和广义线性模型(Mccullagh 和 Nelder,1989)提出的,其基本想法是为了研究更广泛的一类统计模型,其中因变量服从对称分布,且均值和线性预测之间为任意的联系函数。当联系函数为恒等函数而分布为正态分布时,则退化为正态线性模型这一特殊情形。Villegas 等(2013)讨论广义对称线性模型,利用迭代方法给出了该模型的极大似然估计,并利用 Cook(1986)的方法对此模型进行了局部影响分析,以研究极大似然估计加权扰动、因变量扰动等具体扰动模式下的敏感性。#p#分页标题#e#
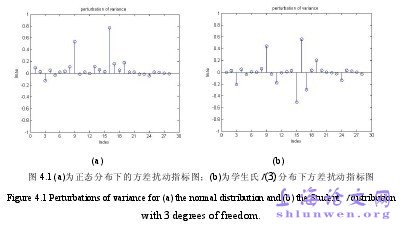
…………..
总 结
本文主要研究了统计模型中有偏估计及带约束统计模型的局部影响分析。具体的研究成果如下:
(1)在线性模型方面,首先,类似有偏估计的比较方法,我们在均方误差矩阵下分别比较了统一有偏估计的残差、几乎无偏统一有偏估计的残差和最小二乘估计的残差,证明了最小二乘残差的方差矩阵小于统一有偏估计的残差、几乎无偏统一有偏估计的残差对应的方差矩阵,得到了统一有偏估计的残差、几乎无偏统一有偏估计的残差优于最小二乘估计的残差的充要条件。其次,研究了两参数估计下的线性模型的局部影响分析,得到了方差扰动、因变量扰动、自变量扰动三种扰动模式下的广义影响函数和广义 Cook 统计量。最后,研究了带随机约束的线性模型的岭估计下的局部影响分析,利用建立扩大模型的方法,得到了此模型的极大似然估计,并成功地将两种基于相应的似然函数的局部影响方法推广到了带约束的有偏估计下,给出了三种扰动方式下的诊断统计量。上述所提方法均通过实例分析,说明验证了我们取得的理论结果。
(2)在椭球线性模型方面,研究了带等式约束的椭球线性模型的局部影响分析。首先利用惩罚似然函数和迭代计算给出了此模型的估计。其次基于惩罚似然函数给出了三种扰动方式下的诊断统计量,推广了基于似然函数的局部影响分析方法。最后给出实际算例说明我们的方法。
(3)在广义线性模型方面,研究了此模型岭估计下的局部影响分析。首先介绍了广义线性模型及其岭估计。其次通过定义此模型的似然距离,将基于似然函数的局部影响分析方法推广到了此模型的有偏估计下,得到了加权扰动、自变量扰动、关联自变量扰动、因变量扰动这四种扰动方式下的诊断统计量。最后用实证说明了我们的方法。
…………
参考文献(略)

