电气工程及其自动化论文哪里有?本文的主要贡献如下:(1)提出了邻点融合算法,以适应复杂的背景。传统的预处理阶段主要以 BLOB图像处理为主,但是在复杂背景下,传统的预处理流程鲁棒性不高,因此提出了邻点融合算法,对二维码进行粗定位,有效滤除了复杂的背景。
第 1 章 绪论
1.3 国内外研究现状
对于 DM 或 QR 二维码的识别,国内外专家学者主要依据以下技术路线[7~8]来处理二维码,如下图 1.8 流程图所示,本文以图像预处理,特征定位图形提取、二维码区域提取、畸变校正重点进行了研究。
杨絮[9]从人的视觉系统对红绿蓝三种颜色的敏感度不同出发,通过对 RGB 三个分量设置不同的权重系数,将彩色图转化为数据量更小的灰度图。并使用了大津律法对图像进行二值化处理,并使用连续的先开运算后闭运算将图像的噪声点去除。接着采用了逐行逐列扫描方式来记录平面二维码图像中满足 1:1:3:1:1 比例的区域,初步定位出 QR 码的“回”字定位图形,接着从候选区域筛选出满足三个正方形的面积比为9:25:49 的定位图形,求出了二维码的模块单位宽度。最后采用了孔洞填充算法,扫描图像的每一行,每一列,依据特定的约束步长,将二维码图像内的白色像素块填孔成黑色像素块。最后以位置探测图案为起始点,进行区域生长,得到二维码的轮廓区域。
杨絮最后提出了两种畸变形式的校正方法。对于斜视背景下二维码识别,由于相机镜头与二维码所在平面不平行导致二维码发生了几何失真,利用畸变图像的 4 个角点与基准图像对应角点建立反透视变换关系,完成了斜视二维码的校正。对于扭曲情况下的二维码识别,采用了区域增长算法求出了二维码的位置探测图案的 12 个角点,同时也得到了二维码的三个角点。接着采用了搭桥法对外轮廓曲线拟合,以上边界为例,选择合适长度的板桥,从最左端开始,记录与二维码外轮廓的切点,并对关键点中过于密集的点进行滤除,将剩下的边界点采用加权最小二乘法拟合,并加大角点的权重,得到边界曲线方程,从而获得二维码的最后一个边界点。再通过积分运算求出了校正图像上的对应点之间的距离关系,最后采用了非线性变换关系,得到校正图像。识别率在复杂背景下达到了 95%,扭曲情况下达到了 90%。从校正效果来看,作者在对曲面二维码的边界线进行拟合时,采用了二次函数拟合,但是对于扭曲严重的情况可能不适用,需要更高次的函数来拟合边界曲线。
第 3 章 轮对零部件二维码特征定位
3.1. 车轴轴端二维码特征定位
3.1.1 车轴轴端 QR 码位置探测图像定位
依据 QR 二维码最初的设计原则,图像平面状态下位置探测图形的黑白像素[29]比例满足 1:1:3:1:1,对每行每列的灰度值进行扫描[30],定位出满足该比例的像素段,具体步骤如下:
(1)逐行扫描预处理之后的图像,判断后一像素减去前一像素的值,如果差值为0,则认为这两个位置的像素是一样的,判断基数增加 1;如果差值为 1,则认为这两个位置的像素值发生了变化,记录此判断基数。直至扫描完该行;
(2)逐列扫描预处理之后的图像,判断方法同步骤(1);
(3)对逐行,逐列记录的基数进行四舍五入,将满足该比例的像素段记录下来,并标记满足该比例的中点坐标。位置探测图形定位算法流程如下图 3.1 所示:
与 QR 码不同的是,对其定位图形来说,DM 码定位图形位于二维码边界,且定位图形的“L”边是实线边界,通过对实线边缘提取可以对 DM 码进行精确定位。霍夫变换对旋转的 DM 码中的“L”型边界也可以检测到,其通过检测原图像的线性特征进行提取,假设直线的斜率为 k ,截距为b 。Hough 变换[31]的基本原理在极坐标系下的同一直线的斜率和截距相同,就可以将像素坐标系中原始图像上的点投影到直线参数空间 ( k,b)中,如下图 3.5 所示为两种坐标系中的对应关系。其原始图像中的点经过投影变换成为参数空间中的曲线,计算在参数空间各个点的曲线的数量,当曲线的数量足够的多时,可以认为是一条直线。
第 5 章 轮对零部件二维码识别实验及分析
5.1 轮对零部件二维码识别系统的实现
为了验证本文的解码算法流程,搭建了二维码识别系统。所使用的摄像机品牌为MER-1070-10GM,二维码种类包括 DM 二维码和 QR 二维码两种,刹车盘所使用的码制大小为 1.5cm×1.5cm,其余零部件所使用的码制大小为 3cm×3cm。视觉系统硬件相关参数如下表所示:

5.2 算法识别效果对比分析
5.2.1 车轴轴端二维码实验分析
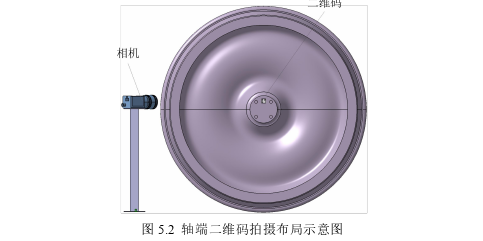
在实验中,二维码粘贴在轴端任意位置,摄像机光轴与轮对车轴轴线成一定角度拍摄二维码所在区域,其中光源未画出。车轴轴端二维码与相机的布局示意图如下图5.2 所示。
对本文两种二维码的斜视校正算法的识别率分析,QR 二维码的总识别率在 93%,DM 二维码在 95.67%。DM 二维码的识别率要比 QR 二维码要高 2.67%。对两种二维码的算法流程分析,这两种二维码虽然都是以 4 个角点做校正,但是 QR 二维码的角点获取方式相较于 DM 二维码复杂。比如 QR 二维码需要扫描每一行每一列满足1:1:3:1:1 的区域来定位位置探测图案,而且还需要进一步确定二维码的外角点,相较于 DM 二维码的 HOUGH 直线检测算法复杂度高。在车轴轴端上建议粘贴 DM 二维码,有利于识别率的提高。
第 6 章 总结与展望
6.1 论文工作总结本文就长春轨道客车厂轮轴车间立体库中遇到的二维码识别进行读取研究。对二维码的两个应用场景:车轴轴端畸变和曲面轮对零部件畸变下的二维码识别展开了研究。对已有的二维码校正技术提出了自己的见解,本文的主要贡献如下:
(1)提出了邻点融合算法,以适应复杂的背景。传统的预处理阶段主要以 BLOB图像处理为主,但是在复杂背景下,传统的预处理流程鲁棒性不高,因此提出了邻点融合算法,对二维码进行粗定位,有效滤除了复杂的背景。
(2)提出了 BP 神经网络的二维码角点分类算法,尽可能多将二维码内部角点滤除。对二维码内部的角点分析,可以将二维码的角点分为十类,有一些角点只存在于二维码的内部,在边界直线拟合阶段,我们只需要边界的角点参与到拟合过程中,为了减小角点搜寻的计算量,采用 BP 神经网络将只属于二维码内部的角点滤除。
(3)提出了搭桥法对曲面轮对零部件的 DM 二维码虚线边缘关键点求解算法。以1.5 倍长的板桥从实线边缘顶点出发,开始向二维码虚线边缘搭建,求出虚线边缘上的关键点。
(4)提出了 CSPSO(粒子布谷鸟算法)对畸变方程组的求解,由于传统的布谷鸟搜索算法收敛速度慢,且收敛精度不高,将粒子群的个体学习因子和社会学习因子引入到布谷鸟迭代后期,有效地弥补了布谷鸟搜索算法莱维飞行的随机性引起的收敛速度慢等问题,提高了最优解的寻优精度与速度。
参考文献(略)

