电力论文哪里有?本文在风电功率滚动预测、分布式实时优化架构、滚动优化模型以及分布式优化算法等方面进行了一定研究,但在研究内容方面仍存在诸多不足,未来仍需要对以下几点做深入研究:(1)大量 EV 接入电网中,会改变电网的潮流分布,有可能增大网络损耗甚至导致电压越限,本文在进行滚动优化时,未考虑网损、电压等指标,后续应考虑涉及电能质量的指标。(2)本文针对滚动优化的研究内容不够充实,没有分析滚动优化时间窗的不同对调度结果的影响
1 绪论
1.2 国内外研究现状
1.2.1 风电功率预测研究现状
风电功率预测按预测时间尺度分为:①超短期预测(以“小时”作为预测时间尺度);②短期预测(以“天”作为预测时间尺度);③中期预测(以“天到月”作为预测时间尺度);④长期预测(以“月到年”作为预测时间尺度)。超短期预测的结果一般用来安排机组的组合顺序并制定短时的发电计划,短期预测的结果可作为电力系统实时调度的基础数据,中期预测的结果可用来安排风电场的季度发电计划或检修计划,长期预测的结果主要应用于地区的规划问题,在对风电场进行选址、定容时评估地区的年均发电量。受各种不确定因素的影响,以月或年为时间尺度的预测难度较大,因此目前研究主要集中在以小时或天为时间尺度的超短期预测或短期预测[21]。
风电功率预测的方法可按是否采用数值天气预报(NWP)进行分类。不采用 NWP 而基于时间序列预测时,预测精度较低,所以现在普遍采用 NWP 预测风电功率,采用 NWP时,可分为物理方法和统计方法,前者不需要风电场历史数据,而后者需要。物理方法是建立在风电功率与气象数据有关联关系的基础上,利用 NWP 得到的气象预测数据,根据风电功率与各气象指标的关联关系对应得到风电机组的输出功率,其中,关键的两个因素是:①一定要能获得风电场全面的物理信息;② NWP 数据务必要准确。在保证以上两点后就可以利用物理信息对风电场所在地建模,最后利用 NWP 获得预测信息,对于刚投产的风电场来说,这种方法是最简单的。而统计方法由历史数据得到气象与风电功率间的关系后,再利用实时数据和 NWP 信息预测风电功率,采用这种方法的前提是要收集风电场至少一年的历史气象数据和运行数据[22]。接下来比较几种常见的统计方法[23],持续预测方法是先预测风速,再间接得到输出功率的一种简单的且易实现的方法,该方法不区分风速信号中的高频和低频分量,并认为下一点的预测值就是最近一点的风速值,因此前、后风速数据相似度低时,采用持续法会产生较大的局部误差,一般来说,相似度低的成分包含在高频分量中。

3 滚动优化调度模型及分布式优化方法的研究
3.1 滚动式动态调度
对风电和 EV 接入电网信息采用滚动预测模型,计算每一时刻的调度策略时,滚动优化只需考虑滚动优化时间窗内的性能。若选取 1 小时为滚动优化的调度周期,滚动优化时间窗为 8 小时,此时滚动优化的时间变化如图 3-1 所示。即每次优化调度为此时刻和未来7 小时的风电和 EV 制定相应策略。
着大量 EV 接入电网充电,在同一时刻接入充电站的 EV 数量增多,集中式调度模式下每次优化需要大量的 EV 信息且计算量增大,导致优化模型求解时间变长,甚至出现求解困难的现象。集中式统一优化车辆充电负荷时,未考虑不同车主的充电意愿,需要车主完全按照优化指令进行充电。此外,单辆 EV 的充电功率达不到能够加入电力市场的门槛[63]。因此,可以考虑将 EV 负荷聚合体作为电力调度部门和单辆 EV 之间的中介,建立包含电力调度、EV 负荷聚合体和分散的 EV 在内的调度模式,从而实现分层分区调度。分布式控制方式指 EV 依据车辆信息和充电电价自主制定充电计划,其优势是计算任务由单台 EV 完成,能有效的减少控制中心的计算时间,同时由于 EV 车主能够根据各自意愿自主制定充电计划,充电计划更容易被车主接受。随着电力电子技术和通信技术的完善和发展,在设备上实现分布式控制已经不是一个难题[64]。
4 算例分析
4.1 算例数据
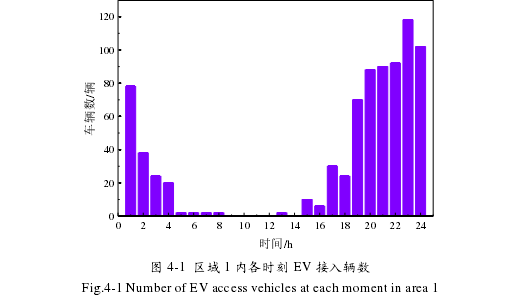
本文利用某区域电网作为算例,该区域有 N(N=2000)辆 EV。根据地理位置的不同,将 N 辆 EV 划分到 A(A=3)个区域。由于各区域地理位置不同,EV 车主职业不同,必然导致 EV 的数量和车主充电习惯的差异。因此本文假设区域 1 有 800 辆 EV 可参与电网调度,且 EV 负荷聚合体位于自由职业者居多的商业区,EV 接入电网的时间在 24 小时内服从2N(23, 2.79 ) 的正态分布,在此区域充电的 EV 的最大充电功率为 6kW,电池容量为26kW•h。区域 2 有 600 辆 EV 可参与电网调度,且 EV 负荷聚合体位于居民区,EV 接入电网的时间在 24 小时内服从2N(17.6,3.4 ) 的正态分布,在此区域充电的 EV 的最大充电功率为 8kW,电池容量为 36kW•h。区域 3 有 600 辆 EV 可参与电网调度,且 EV 负荷聚合体位于工薪阶层居多的商业区,EV 接入电网时间在 24 小时内满足 U(9,14)、U(17,21)的均匀分布,在此区域充电的 EV 的最大充电功率为 10kW,电池容量为 48kW•h。EV 运营商向车主提供的充电费用折扣率 为0.5,EV 充电单价chargep 为 1.5 元。车主偏好系数pre 在日间(07:00~20:00)服从 U(0,0.4)的均匀分布,在夜间(20:00~07:00)服从 U(0.5,1)的均匀分布。同时假设 EV 充电结束时,电量均已满,EV 充电桩效率为 90%,每辆 EV 接入电网时的初始荷电状态0SOC 服从2N(0.3,0.1 ) 的正态分布,通过蒙特卡洛随机抽样方法,可以得到各区域各时刻接入的 EV 个数,如图 4-1—4-3 所示。表 4-1 为分时电价表。
4.2 算例结果分析
4.2.1 滚动优化模型结果分析
运用改进 ADMM 算法和改进 GWO 算法对滚动优化模型进行求解。图 4-4 为 EV 优化充电与无序充电各时刻总负荷功率对比。由于目前 EV 接入电网充电时刻与常规负荷用电高峰期的重叠,使得优化难度增大。但从图 4-4 可以看出,在 09:00~15:00 和 19:00~22:00日间负荷高峰期,优化后负荷总功率降低,在 00:00~07:00 夜间负荷低谷期,优化后负荷总功率升高。由此可见 EV 有序充电比无序充电系统总负荷的峰谷差小。
无序充电时,EV 接入电网后立即充电,即插即充的情况,此时 EV 运营商无需采用激励机制引导 EV 的充电计划,也就无需支付给车主激励费用,运营费用只包含向电网购电的费用。由图 4-7 可以看出,与无序充电相比,在日间进行有序充电时,EV 运营商在每一小时的运营费用普遍低,主要是由向电网购电的电价起作用,通过优化 EV 的充电计划,在电价低的时段进行充电,减小了购电费用,此时虽然增加了激励费用,但减小的购电费用能够完全冲抵增加的激励费用,运营费用也比无序充电时要低。与无序充电相比,在夜间进行有序充电时,EV 运营商在每小时的运营费用普遍高,主要是由于夜间本身接入电网的 EV 较少,激励费用的影响较大。此时虽然运营费用较大,但通过采用激励措施,可以提高车主的充电满意度。
5 总结与展望
5.1 总结
针对在对电网进行优化调度时,风电功率难以准确预测,EV 在充电时信息通讯量大以及 EV 车主可能会遭受隐私泄露等问题。搭建以电网电源侧、EV 负荷聚合体和 EV 车主为主体的分布式框架,在此框架基础上对电网实现滚动优化调度,以达到满足电网多方主体利益的目的。所取得的研究成果包括:
(1)基于风电场的历史数据,建立风电功率滚动预测模型。
风力出力大小易受自然环境的影响,采用基于误差修正的 BP 神经网络模型对风电功率进行滚动预测,并将此模型与单一的 BP 神经网络模型在采用相同样本下的预测结果进行对比分析,得出此模型预测精度高的结论。同时为了考虑风电功率预测误差的波动性,分析利用建立的预测模型预测时产生的误差的分布特征,在给定置信度的条件下,求出风电功率预测值波动范围为后续风电的调度提供了基础数据。
(2)对不同区域的 EV 进行差异化建模。
由于各区域所处的地理位置和车主工作性质不同,必然导致车主行驶习惯和充电方式不同。根据不同区域车主使用 EV 的特征,进行了差异化建模。
(3)用 ADMM-IGWO 算法对优化模型进行求解。
建立了考虑风电功率预测误差和 EV 预测信息的 EV 实时滚动优化模型,以达到平抑电网的负荷波动、提高风电消纳量、减小 EV 运营商运营成本和提高 EV 车主充电满意度为目的,将改进 ADMM 算法和改进 GWO 结合起来求解模型。模型求解时将一个庞大的优化问题分解成几个小问题,求解过程无需全局协调同步迭代,信息只在两个主体之间交换,通讯量少,数据的冗余度小。算例结果表明,采用的方法解决了含有多个子问题的模型并保持了收敛性。算法的适应度高,适用面广,计算速度快,能够满足未来电网通讯的要求。
参考文献(略)

