电力论文哪里有?本文针对低载波比条件下永磁同步电机无传感器驱动系统的滑模观测器进行分析和研究,旨在提高低载波比条件下滑模观测器的稳定性和观测性能,从而促进永磁同步电机无传感器驱动系统在低载波比工业场合中的实施。针对低载波比条件下 SMO 存在的局限性研究了相应的改进方案,并基于 2.1-kW SPMSM 控制系统平台进行了实验验证。
1 绪论
1.2 永磁同步电机无传感器控制方法的国内外研究现状
众多变频器厂家和高校研究机构已经针对永磁同步电机无传感器控制方法在工业生产、民用家电和装备制造的实际应用问题进行了深入研究,并取得了成功应用。在通用变频器领域,一些国内外变频器品牌如瑞士 ABB 的 ACS580 系列、日本安川 GA500 系列、台达CH2000系列和汇川MD500系列等变频器已经完成了无传感器控制模式的集成。因此,永磁同步电机驱动的无传感器控制方法凭借成本降低、系统小型化和可靠性增强等竞争优势愈发成为交流电机驱动领域的发展潮流。
永磁同步电机驱动的无传感器控制方法发展至今,仍没有一种能够囊括电机全转速范围内均达到较高精度的转子位置和转速估计方法。目前,无传感器控制方法根据电机转速运行速域,一般分为零/低速和中高速两种,如图 1-1 所示。其中,零速/低速方法依据电机凸极特性通过外加激励获得位置信息,中高速方法依据电机基波模型求取位置信息[11]。

3 基于 SMO 的 SPMSM 无传感器控制方法
3.1 滑模变结构理论
变结构理论最早由前苏联 Emelyanov 等人提出,Utkin 和 Young 等学者相继对滑模变结构控制和滑模控制的相关理论进行了研究与拓展[64]。滑模控制是根据所设计的控制律对系统状态进行调整,以此实现系统状态按照人为规划的轨迹进行运动,从而对传统线性控制受参数变化及外部扰动等不利因素影响的抑制。
滑模观测器是基于变结构控制思想而衍生的一种状态观测器,因此它具有不连续且非线性控制的特性,造就了其对被控对象内部参数变化及外部扰动具有免疫作用,这是其它位置观测器无可比拟的。此外,因其特殊的滑动特性,当控制系统处于滑动模态滑动时,其滑动状态不会受外界环境或被控对象等不利因素而改变运动轨迹,这使得其具有快速的动态响应。然而,凡事都具有两面性,由于变结构控制的不连续开关特性也造成了其不可避免的抖振现象。
抖振现象产生的原因包括:1)在实际控制系统中,由于数字控制系统存在执行延迟,系统状态输入量与控制作用无法同时实现,而且控制量的衰减也会造成抖振;2)由于系统存在惯性,其控制作用不能实现无穷增益,则会存在时延;3)因系统状态输入量存在采样偏差,将会使系统不稳定;4)因离散系统本身存在的截断误差,不能确保滑动模态的切换动作完全在滑模面上。通过对以上抖振产生原因的剖析,若不消除滑模控制系统中存在的高频抖振,控制系统的稳定性及准确性则无法获得保障,因此,抖振现象的抑制方案则显得不可或缺。
5 基于 SMO 的 SPMSM 低载波比无传感器控制实验验证
5.1 矢量控制系统实验平台简介
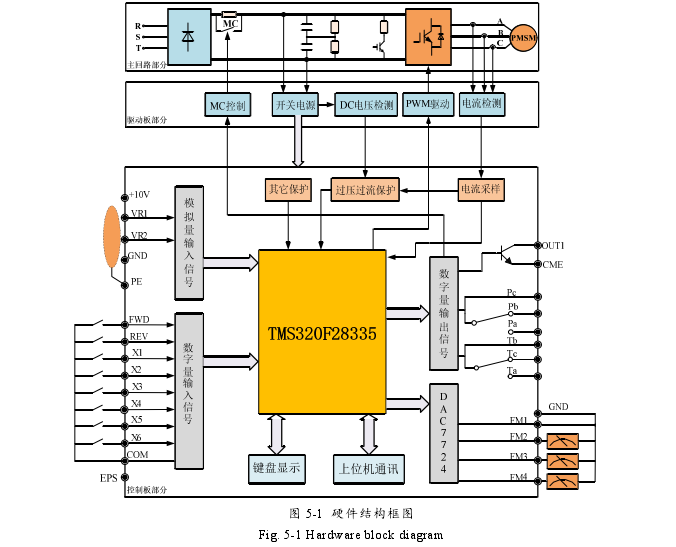
为了验证本文所提出的无传感器驱动策略的可行性,搭建了 2.1-kW 表贴式永磁同步电机矢量控制实验平台,图 5-1 是电机驱动控制系统的硬件结构框图,系统的控制核心是 TMS320F28335 芯片。
5.2 基于 DAVPI-SMO 的 SPMSM 低载波比无传感器驱动系统正确性验证
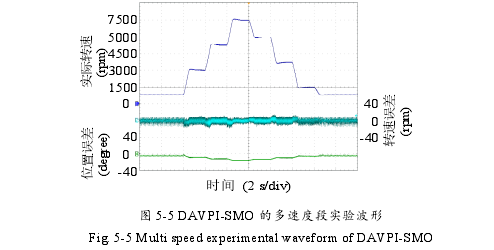
为了验证本文提出的基于DAVPI-SMO的SPMSM低载波比无传感器驱动策略的正确性,基于DAVPI-SMO方法的多速度段实验波形如图5-5所示,电机给定转速指令包括750 r/min ~ 3000 r/min ~ 4750 r/min ~ 7500 r/min ~ 5000 r/min ~ 3250 r/min ~ 1500 r/min ~ 750 r/min的加速上升阶段和减速下降阶段,整个过程展示了10%最大转速至100%最大转速范围内的电机运行状况,且各给定转速指令之间的加速或减速时间均为0.2 s。从实验结果可知,本文所提出的无传感器驱动策略在电机中高速范围的多转速段内均具有良好的转速跟踪能力。
6 结论
6.1 总结
转子位置和速度信息对于高性能交流电机驱动系统至关重要。由于成本降低、系统小型化和可靠性增强等竞争优势,永磁同步电机驱动的无传感器控制方法越来越受到学术界和工业应用的关注。然而,仍有一些工业场合存在的极端问题限制了永磁同步电机无传感器驱动系统的应用。本文针对低载波比条件下永磁同步电机无传感器驱动系统的滑模观测器进行分析和研究,旨在提高低载波比条件下滑模观测器的稳定性和观测性能,从而促进永磁同步电机无传感器驱动系统在低载波比工业场合中的实施。针对低载波比条件下 SMO 存在的局限性研究了相应的改进方案,并基于 2.1-kW SPMSM 控制系统平台进行了实验验证。 本文完成的主要工作和结论如下:
(1)建立了 SPMSM 在 A-B-C 坐标轴、α-β 坐标轴和 d-q 坐标轴下的标量数学模型,在此基础上,利用复矢量形式构建了 SPMSM 的复矢量数学模型,从而降低了系统阶数,简化了控制系统分析步骤。其次,通过求解 SPMSM 复矢量数学模型的微分方程,推导了静止坐标轴下的 SPMSM 精确离散化数学模型,该模型考虑了数字控制系统时延和数字实现的离散化截断误差效应的影响,而且为后续实现低载波比条件下 SMO 的理论研究和分析奠定了基础。
(2)回顾了滑模变结构控制理论,并基于 SPMSM 复矢量模型设计了传统 SMO,并进行了稳定性分析。考虑固定的滑模增益无法满足电机在宽速范围内无传感器运行,设计了同电角速度变化的滑模增益,以满足无传感器宽速范围运行的性能需求。此外,分析总结了 SMO 的抖振产生原因以及相应的解决策略,同时分析了低载波比条件下SMO 存在的缺陷,为后续 SMO 在低载波比工况下的应用提供了改进思路。
(3)针对 SMO 存在的缺陷,提出了一种基于自适应矢量 PI 的 SMO。自适应矢量PI 在中心频率处的高增益可以代替符号函数实现定子电流的无静差跟踪,而且可以利用自身选频特性滤除观测反电势信号中除基波运行频率之外的其它次谐波分量,进而省略了 LPF。其次分别在连续时间域和离散时间域内对自适应矢量 PI 滑模观测器进行建模和观测器控制参数设计,并对两种不同的设计方案进行了稳定性分析,其结果表明了直接在离散时间域内对观测器建模和参数设计可以显著提高滑模观测器在低载波比工况下的稳定性。
参考文献(略)

