不均衡数据聚类算法及其在电力变压器状态评估中的应用

用聚类算法分析电力变压器不均衡监测数据，可以快速提取“异常/故障”数据，用于后续状态评估。但经典的聚类算法没有考虑类簇规模对聚类结果的影响，算法会使得少数类类簇的簇心被多数类类簇的样本“吸引”发生偏移，最终算法会将多数类类簇的数据错误地划分至少数类类簇。改进传统聚类算法，改善算法对不均衡数据的聚类性能对于提高电力变压器状态评估精度有着重要意义。本文为解决上述问题，提出了基于相邻区域样本不均衡度量的改进 FKM 算法和基于交叉边界样本不均衡度量的改进 RFKM 算法。这两个算法，都将类簇包含的样本数纳入到样本隶属度计算之中，使得样本隶属度不仅与样本和簇心的距离有关，还与类簇间的不均衡度有关。改进 FKM 算法通过融合类簇规模的改进模糊隶属度函数对相邻区域的样本进行度量，降低了多数类类簇中与少数类类簇相邻区域的样本对少数类类簇簇心的“吸引”程度，保证了少数类类簇的簇心始终处于较为合理的位置，改善了 FKM 算法对不均衡数据的聚类效果。改进RFKM算法引入考虑类簇规模不均衡度量的改进模糊隶属度函数对交叉边界区域的数据样本进行分析处理，改善了 RFKM 算法对电力变压器不均衡监测数据的聚类效果

........

第一章 绪论

通过分析电力变压器监测数据，对其运行状态进行评估，及时发现其状态变化及存在的安全隐患，可以带来以下几方面的效益：（1）有助于检修人员掌握变压器运行状态，及时维护异常设备，延长电力变压器使用寿命。（2）电力变压器故障会导致电力供应中断甚至造成大面积停电事故，电力变压器状态状态评估有助于运维人员及时确定故障类型和位置，及时更换故障设备，保障电力供应。（3）电力变压器状态评估结果有助于运维人员制定合理的检修计划，缩短因检修造成的停电时间。目前我国电力变压器状态评估主要集中在电力变压器故障诊断和状态检修方面。随着电力变压器状态评估要求的提高，已经不能仅仅分析故障录波设备采集的故障数据，进行故障诊断，更要全面分析电力变压器监测数据，及时发现其状态变化和可能存在的安全隐患，进而制定合理的检修计划，保障电力供应。随着我国智能电网建设的推进，物联网技术在电力系统广泛应用，监测设备每天都产生海量的不均衡监测数据，包括占绝大多数的正常运行状态数据和低密度的故障状态数据，形成了电力变压器不均衡监测数据集[3-5]。

第二章 相关背景知识介绍

2.1粗糙集理论

自然界和人类社会活动的各种现象都可以归结为两类：确定性现象和不确定性现象。确定性现象是指在一定的条件下必然会发生的现象；不确定性现象是指在满足一定条件也不一定会发生的现象。不确定现象主要具有以下几个特性：（a）随机性：事物的因果关系不确定，从而导致结果的不确定性。针对随机性，人们用概率来度量，概率表示事件发生可能性的大小。概率理论是从随机性中把握广义的因果关系。（b）模糊性：事物在本质上没有明确的含义，在量上没有明确的边界，导致事件呈现“亦此亦彼”的状态，是事物类属关系的不确定性。针对模糊性，人们用隶属度来度量，隶属度表示事物多大程度属于该类簇。（c）粗糙性：描述事物的信息（知识）不充分、不完全，导致事物间的不可分辨性。粗糙集中的不确定性是基于一种边界的概念，当边界区域为空集时，问题变为确定性的。粗糙集理论的提出为人们提供了处理事物信息不充分、不完全情况下的各种问题的数学工具，极大促进了不确定性数学问题的解决。

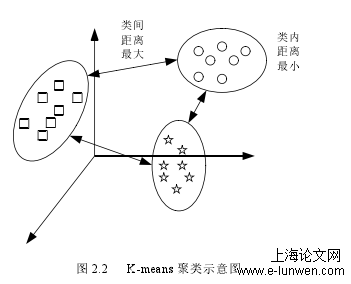
2.2聚类算法

粗糙 K-means 算法经过众多学者的改进已经能较好地处理边界模糊、有交叉的数据集，但其没有在算法层面考虑类簇规模的不均衡，所以处理不均衡数据集时效果较差。但作为重要的无监督学习算法之一，用聚类的方法去研究不均衡数据集，有着重要的意义。因此，针对不均衡数据集的聚类算法的研究成了近年的热点。本章主要介绍了粗糙集理论、聚类算法的基础理论和粗糙模糊 K-means 算法及其相关改进算法。粗糙集引入了上、下近似集的概念，将数据样本划分至确定属于该类簇的下近似集和可能属于该类的边界区域，很好地解决了模糊数据的归属问题。聚类算法是利用数据样本间的距离将数据样本划分到不同的类簇，从而达到类间相似度低，类内相似度高的目标。最后介绍了粗糙模糊 K-means 聚类算法及其改进算法的原理和步骤，粗糙模糊 K-means 算法很好地集合了粗糙集和模糊集的优势，对边界区域的样本进行更加精确的度量，提高了边界模糊数据集的聚类性能。

第三章 基于相邻区域样本不均衡度量的改进 FKM 算法....................... 18

3.1类簇相邻区域样本的改进模糊度量 .................... 18

3.2基于相邻区域样本不均衡度量的改进 FKM 算法...................... 21

3.3实验分析...... 22

第四章 基于交叉边界样本不均衡度量的改进 RFKM 算法.................... 26

4.1类簇交叉边界样本的模糊度量 ............................ 26

4.2基于交叉边界样本不均衡度量的改进 RFKM 算法................... 29

4.3 实验分析...... 30

第五章 基于聚类算法的电力变压器状态评估方法.......... 39

5.1引言.............. 39

5.2基于聚类算法的电力变压器状态评估 ................ 40

5.3实验分析...... 44

第五章 基于聚类算法的电力变压器状态评估方法

5.1引言

但随着我国智能电网建设的加快，以及物联网技术在电力系统中广泛应用，监测设备产生了海量的不均衡监测数据。一方面传统的方法更多的集中于对已发生故障的设备进行故障诊断；另一方面传统的方法已经不能快速准确地处理海量的监测数据。同时，新兴的人工智能方法的研究主要集中在有监督学习领域，要求利用大量的已知标签的历史数据去训练模型，再用于状态评估。有监督学习算法固然可以对电力变压器状态进行评估，但因其不可复制性，即对于每一台电力变压器都要进行训练生成模型，不利于大规模推广。其次，在某些特定的场合，需要从海量的监测数据中提取出低密度的异常/故障数据给专家进一步分析，有监督学习算法显得力不从心。而作为无监督学习领域的经典算法之一，聚类算法可以快速准确地对海量数据进行预处理，同时也可以进一步的对电力变压器的状态进行初步的评估，给出评估结果。电力变压器状态评估总体结构如图 5.1。

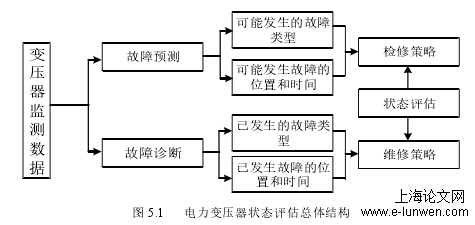
5.2基于聚类算法的电力变压器状态评估

建立一个合理、有效的的指标体系对于变压器状态评估至关重要。电力变压器作为一种复杂的多参数电磁系统，指标繁多，常用的指标有化学试验指标和高压试验指标。国家电网公司也提供了相应的指标体系，但该指标体系较为繁琐，每个故障类型涉及的指标冗杂，也有学者专门对指标体系的建立进行了研究。为了更加准确地评估变压器的运行状态，本文引用了文献[52]简化的故障对应指标类型如表 5.1。该指标体系参考 DL/596-1996《电力设备预防性试验规程》和 GB/T7252-2001《变压器油中溶解气体分析和判断导则》，以及国家电网公司制定的《油浸式变压器（电抗器）》状态评价导则（Q/GDW169-2008），具有一定的合理性和准确性。

参考文献

[1] 张东霞, 苗新, 刘丽平, 张焰, 刘科研. 智能电网大数据技术发展研究[J]. 中国电机工程学报, 2015,35(01): 2-12.

[2] 江秀臣, 盛戈皞. 电力设备状态大数据分析的研究和应用[J]. 高电压技术, 2018, 44(04): 1041-1050.

[3] 张东霞, 苗新, 刘丽平, 张焰, 刘科研. 智能电网大数据技术发展研究[J]. 中国电机工程学报, 2015,35(01): 2-12.

[4] 严英杰, 盛戈皞, 陈玉峰, 江秀臣, 郭志红, 杜修明. 基于大数据分析的输变电设备状态数据异常检测方法[J]. 中国电机工程学报, 2015, 35(01): 52-59.

[5] 廖瑞金, 王有元, 刘航, 刘宏波, 马志鹏. 输变电设备状态评估方法的研究现状[J]. 高电压技术, 2018,44(11): 3454-3464.

[6] Wang M H, Huang C P. Novel Grey Model for the Prediction of Trend of Dissolved Gases in Oil-filled Power Apparatus[J]. Electric Power Systems Research, 2002, 67(1):53-58

[7] Nafar M, Niknam T,Gheisari. Using Correlation Coefficients for Locating Partial Discharge in Power Transformer[J]. International Journal of Electrical Power & Energy Systems,2011,33(3)：493-499.#p#分页标题#e#

[8] Chawla N V, Bowyer K W, Hall LO, et al. SMOTE: synthetic minority over-samplingwww.zhonghualw.com technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357.

[9] Han H, Wang W Y, Mao B H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning[C]. International Conference onAdvances in Intelligent Computing. 2005.

[10] Barandela R, Valdovinos R M, Sánchez J S, et al. The Imbalanced Training Sample Problem: Under or over Sampling[C]. Structural, Syntactic, and Statistical Pattern Recognition, Joint IAPR International Workshops,SSPR 2004 and SPR 2004, Lisbon, Portugal,August 18-20, 2004: 806-814.

.........