本文是一篇电力论文,电力的产生方式主要有:火力发电(煤等可燃烧物)、太阳能发电、大容量风力发电技术、核能发电、氢能发电、水利发电等。(以上内容来自百度百科)今天为大家推荐一篇电力论文,供大家参考。
第一章 绪 论
1.1 研究背景与意义
我国拥有广阔疆域,但能源资源分布与经济贸易发展水平却并不协调。沿海地区作为我国的通商口岸一直具有稠密的人口分布,交通与贸易的便利使得其经济发展较为迅速,但自然资源的匮乏却制约着其经济的进一步发展。而我国可用于发电的一次能源却主要分布在中西部,比如云南、贵州地区丰富的水利资源以及新疆、山西、陕西等地区丰富的煤矿资源。但这些区域的经济发展程度相对较低,用电需求量不高,与沿海地区形成鲜明对比。因此,在我国实施大范围跨区域的输电工程势在必行,而“西电东送”工程就是在这种背景下被提出的。与传统的交流输电技术相比,高压直流输电(High-voltage Direct Current, HVDC)由于在大规模远距离电能传输方面可以实现更好的经济效益,并且在可靠性、调控灵活性方面也具有更优秀的表现[1-3],因此一直在“西电东送”工程中占据重要地位。截止 2016年底,国家电网已经建成“六交五直”特高压交直流输电网架[4],南方电网也形成了“八交十直”交直流输电系统。这些直流输电工程的受端落点多是选择在东部沿海发达地区,例如华北、华东[5-6]以及广东电网[7],而伴随远景年更多 HVDC 的投产与馈入,东部沿海地区典型的多直流馈入电网将变得更加复杂。多直流馈入交流电网具有直流送电比例高,负荷集中度高,各直流电气耦合紧密等特点。一旦受端交流系统发生故障,该故障带来的影响极易通过耦合紧密的受端电网而波及到其他直流逆变站,引发多个逆变站同时发生换相失败[8]。逆变站在换相失败的故障期间有功与无功会大幅跌落,而在清除故障后的恢复过程中,有功在直流恢复控制系统的作用下逐步恢复,但无功却存在着一个向交流系统大幅吸收的动态阶段[9-11],即便在这个过程中逆变站换流母线的无功补偿装置会提供一定量的感性无功,但叠加之后仍然不足以满足直流系统在该过程中的无功需求[12,13]。一旦交流受端的电压支撑能力不足,直流动态无功需求便会引起直流有功恢复的震荡和迟滞,进而增加交流系统暂态电压失稳和功角失稳的风险。显然,研究交流扰动下多回直流动态行为对电网安全的综合影响并建立有效的评估指标,对交直流电网的规划和运行管理都具有重要意义。
..........
1.2 国内外研究现状综述
1.2.1 交直流系统电压稳定性相关评估指标分析
目前,在评价交直流互联大系统的电压稳定性时,多是直接把针对于该系统分析得到的静态电压稳定分析结果应用到实际包含动态过程的系统中,作为工程上评判系统电压稳定性的标准。这种做法计算简便,易于掌握,便于对系统稳定性做出快速识别,但是该做法并没有考虑各元件的动态过程,只是把达到交直流系统的潮流极限作为稳定判别标准,因此判断结果并不完全准确。文献[14-16]将电压稳定因子(Voltage Stability Factor, VSF)应用于交直流系统中用于判定其电压稳定性。其中 VSF 表示的意义是在某一系统运行方式下,当无功功率发生扰动时所引起的换流母线电压扰动量,当 VSF>0 时,系统被认为是可以维持稳定运行状态,而当 VSF<0 时,则认为该系统难以维持稳定。文献[16]指出其对于交直流系统的电压稳定性判别结果与短路比并不一致,并且也无法如短路比一般给出系统的稳定裕度,所以现在已经较少使用该指标作为评估交直流互联系统电压稳定性的判据了。文献[17,18]则是提出了所谓控制灵敏度(Control Sensitivity Index, CSI),该法优点是可以结合某种特定的直流控制策略来评估交直流系统稳定性,但与 VSF 一样,其同样无法指明交直流系统的稳定裕度,只能作为一个判定系统稳定性的辅助指标。文献[19-21]将特征值法推广到交直流系统中,用潮流雅克比矩阵的最小特征值作为评估系统电压稳定性的指标。该种方法虽然可以给出系统的稳定裕度,但在处理复杂大电网时计算量较大,若系统运行方式以及拓扑结构改变,还需要重新计算指标。文献[29,30]则是使用了换相失败免疫因子(Commutation Failure Immunity Index, CFII)来作为系统换相失败难易程度的判定,同时也可以给出系统强度与稳定性强弱。CFII 的定义与单馈入短路比类似,只是将短路容量中的节点等值阻抗替换为引起换相失败的临界接地阻抗。上述两份文献均指出 CFII 与有效短路比呈线性关系,但由于其判别结果较强,主要是针对换相失败难易程度的评估,因此该指标多是作为对于交直流系统强度判定的辅助指标。
...........
第二章 单馈入系统短路比指标与换流母线暂态电压稳定的关系
本章将先简要介绍单馈入有效短路比 ESCR 的定义,和其对于单馈入系统受端电网静态电压稳定的分析方法以及阈值判别体系。由于该阈值范围是在准稳态模型中计算并给出的,并没有考虑电力系统的动态过程,其能否准确界定直流扰动后恢复过程中的电压支撑能力的强弱尚不明确。因此,本章还将进一步探讨 ESCR 指标在单馈入系统扰动后的动态恢复过程中的相关表现,即其是否能准确反映换流母线暂态电压的稳定性。具体研究方法是在 PSCAD/EMTDC 中的 CIGRE 标准单馈入测试直流系统中,改变用于判别系统是否稳定的 ESCR 临界阈值的某个影响因素,并观察在该影响因素改变时 ESCR临界值的变化情况,以得到结合了 HVDC 动态过程的 ESCR 阈值变化规律和判别体系。同时这部分研究结论也可以和第四章中 MIESCR 在多馈入系统扰动后恢复过程中的临界值变化情况做对照。
2.1 ESCR 的定义及其与最大功率曲线的关系
为了阐明 ESCR 的物理意义,文献[22]还提出了直流最大功率曲线(MaximumPowerCurve,MPC)并阐明了其绘制方法。即在保持换流站补偿电容不变的前提下不断改变直流电流定值,基于直流准稳态模型计算直流功率,形成的 Pd Id关系称为直流最大功率曲线,其中功率最大值称为直流最大传输功率(MaximumAvailablePower,MAP)。中文文献[16]指出如果以额定运行方式为初始点,在不同的系统结构和短路比下可以得到不同的 MPC 和 MAP。当额定运行点位于 MPC 上 MAP 的右侧(斜率为负),即dd d 1d /d |I P I<0时,交流电网为弱系统,直流系统不能保持稳定运行。反之,则系统较强。满足dd d 1d /d |I P I=0 的系统短路比为临界短路比。图 2-2 给出了逆变站采用定熄弧角控制手段且熄弧角γ=18 时 3 种短路比下计算得到的 MPC。受端电网结构、准稳态模型和额定状态下逆变站补偿电容的初始化计算等均同文献[2]。
.........
2.2 换流母线暂态电压完全失稳的判断标准
由于接下来对于指标的探讨涉及到换流母线暂态电压失稳问题,因此将先对该失稳标准予以界定。本文认为,对于计算指标节点的节点电压波形,若在发生故障之后波形产生较为均匀的连续震荡且不能恢复稳定,则可以视之为系统完全失稳的标志,如图 2-3,该图波形中故障开始时间是 2s,并在 2.1s 处切除故障,从图中可以观察到系统在 2.1s后其电压呈周期性失稳,此即为本文认为的系统完全失稳的标志。同时,对于某一没有使系统完全失稳的网架,如果继续增加阻抗会使系统完全失稳,则认为该系统目前保持临界稳定状态,并把该网架称为临界网架,而通过该网架计算得到的 ESCR、MIESCR以及 GMIESCR 的值即为该指标临界值。
...........
第三章 多馈入系统电压支撑能力评价指标的评估与改进 ............17
3.1 MIESCR 的定义及其与最大功率曲线的关系............17
3.2 多直流馈入系统中 MIESCR 的阈值变化.........21
3.3 MIESCR 与 MIMPC 关系的物理解释.......22
3.4 MIESCR 与换流母线电压支撑能力的关系评估........23
3.5 广义多馈入有效短路比(GMIESCR) ........25
3.6 本章小结........27
第四章 GMIESCR 指标中修正系数的计算方法研究 ...........29
4.1 修正系数 K 的几种计算方法...........29
4.2 不同修正系数下指标临界值受临界网架参数的影响程度评估..........32
4.3 直流系统容量对于指标临界值的影响程度评估.......42
4.4 本侧换流母线稳态电压水平对指标临界值的影响程度评估.....45
4.5 本章小结........47
第五章 GMIESCR 指标的实用化计算方法研究 ..........49
5.1 受端短路容量对 K-MIIF 的影响程度评估.......49
5.2 直流系统容量对 K-MIIF 的影响程度评估.......59#p#分页标题#e#
5.3 本侧换流母线稳态电压水平对于 K-MIIF 的影响程度评估......63
5.4 对于合适修正系数 K 的选择...........66
5.5 本章小结........69
第五章 GMIESCR 指标的实用化计算方法研究
上一章中用于计算 GaMIESCR、GbMIESCR、GcMIESCR、GdMIESCR 的 Ka、Kb、Kc、Kd( Kd Ka Kb)值是根据实时仿真数据的计算所得到的,而如果是在实际的大电网情况下,这种计算方法计算量较大,不利于工程应用。因此本章将在上一章的基础上探究 K 值的规律,期望得到一个只需根据网架参数即可计算的修正系数 K 的计算方法。具体方法是探讨受端短路容量、直流系统容量、本侧换流母线稳态电压等因素对 K-MIIF关系的影响,若无影响,那么修正系数 K 就可通过 MIIF 唯一计算得到。以此思路从 Kb、Kc、Kd 值中选择一个适当的 K 值作为计算 GMIESCR 的 K 值,并在合理的误差范围内简化或者拟合计算方法,以达到简化计算 GMIESCR 的目的。其中,由于上一章已经说明 GaMIESCR 在数值上与 MIESCR 差别并不大,对于其临界值的变化改善也不明显,所以本章将不在单独讨论 Ka。
5.1 受端短路容量对 K-MIIF 的影响程度评估
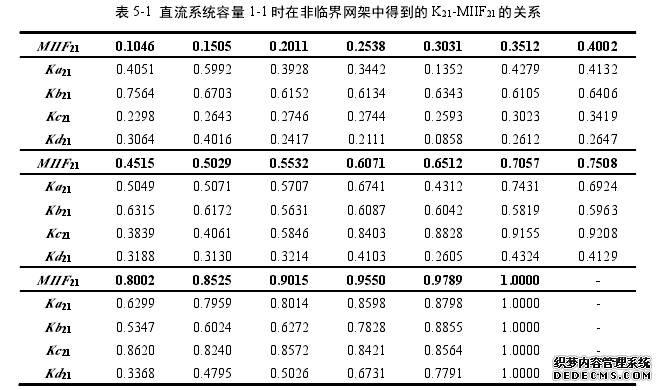
在表 4-6(a)、(b)、(c)中,本文用 MIIF 来表征临界网架参数的变化,那么,网架参数对于 K 值的影响是否可以视为 MIIF 对于 K 值的影响?为便于叙述,本文把使交直流系统处于非临界稳定状态(稳定性较好)的交直流网架称为非临界网架。接下来,本文将在非临界网架中变化MIIF21来得到其对应的K21值,若在这种情况下得到的K21-MIIF21值的关系与相同直流容量情况下临界网架(表 4-6(a)、(b)、(c))得到的 K21-MIIF21值的关系相差不多或者是将前者的数据带入到表 4-6(a)、(b)、(c)计算得到的 GbMIESCR1、GcMIESCR1、GdMIESCR1临界值变化不大,则认为可以将非临界以及临界网架参数对于 K 值的影响视为 MIIF 对于 K 值的影响。综上所述,本节将先探讨非临界网架参数对K 的影响,然后将评估受端短路容量变化(临界网架对应的短路容量小,而非临界网架对应的短路容量大)对于 K-MIIF 关系的影响,这些关系的明确有利于实现根据网架参数直接计算 K 的方法。

...........
结论
本论文对目前电力界比较关心的交直流相互影响的研究方向开展了相关研究。在明晰了 MIESCR 与 ESCR 在多直流馈入交流系统的适用范围以及物理意义的基础上,首次提出了考虑 HVDC 动态恢复过程影响的广义多馈入有效短路比指标 GMIESCR。与在准稳态模型中制定的 ESCR、MIESCR 定义不同,该指标可以结合实际扰动对于受端电压支撑能力给出更准确的评估,对于在工程前期直流落点的选址规划方面具备一定的指导意义。
1.在 CIGRE 标准测试系统中测试了考虑 HVDC 动态行为的 ESCR 的临界值,发现在换流母线处发生严重扰动时,该值小于准稳态模型中根据潮流极限得出的临界值,而直流容量的增加也会进一步减小 ESCR 的临界值,另外稳态电压水平的增加也会降低 ESCR 的临界值水平。根据仿真结果给出了考虑 HVDC 动态行为的 ESCR 在单直流馈入系统中的临界值。若换流母线电压水平保持在额定值以上,当 ESCR<1.1 时,系统电压支撑能力极弱,交直流系统在扰动发生后不能恢复稳定运行;当 ESCR=1.1时,交直流系统在扰动发生后可恢复临界稳定状态;当 ESCR>1.1 时,系统电压支撑能力相对较强,交直流系统在扰动发生后可以回复到稳定运行状态。
2.在 MIESCR 适用范围的基础上进一步明晰了 ESCR 在多直流馈入交流系统的适用范围以及物理意义,即当发生影响多回直流的严重扰动时应采用 MIESCR,而当发生只影响单回直流扰动时应采用 ESCR,ESCR 与 MIESCR 划分了直流电压支撑能力的上下限,并以该两项指标的适用条件为基础构建了 GMIESCR。该指标从定义上统一了 ESCR 与 MIESCR,是这两项指标在多直流馈入系统中应用的推广,具有更广泛的应用范围,即可以结合实际扰动场景更准确的反映受端交流系统对于换流母线的支撑能力。
..........
参考文献(略)

