本文是一篇电力论文,电力工业体制改革和电力工业的发展,需要有相应的电力投资体制改革相配套,在这段时间里,电力建设投资体制最大的变化是由拨款改为贷款;由于电价严重偏低,为了解决电力投资不足,主要采取了建立电力建设基金、卖用电权和集资办电等办法。(以上内容来自百度百科)今天为大家推荐一篇电力论文,供大家参考。
第一章 绪论
1.1 选题背景及研究意义
高压直流输电(High Voltage Direct Current Transmission, HVDC)是以直流电的方式实现能量传输的输电方式。实现高压直流输电,需要在送电端进行整流,在受电端进行逆变,中间的输电线路上为直流电压[1]。由于直流输电在远距离、大容量输电时具有优良的经济性,能够实现非同步并网,输送的有功功率和无功功率可由控制系统控制,海底电缆输电等交流输电所不具有的优点[1; 2],成为现代电力系统的重要组成部分。当前以绝缘栅双极晶体管(Insulated Gate Bipolar Transistor, IGBT)组成换流设备的柔性直流输电(Voltage Source Converter Based High Voltage Direct Current Transmission,VSC-HVDC)快速发展,是实现多端直流、风电场并网的首选技术,然而常规直流输电技术(Line Commutated Converter-HVDC, LCC-HVDC)仍在大容量、远距离、高效率方面略胜一筹[3],在未来的电网发展中不可或缺。并且,由于我国能源与能源需求为逆向分布,发展高压直流输电技术能够在一定程度上缓解能源供应紧张,实现我国经济、能源、环境协调发展[4]。我国直流输电起步晚,发展快。表 1-1 显示,截止到 2015 年,我国已建成投运 26条高压直流输电工程,其中有 6 条为±800kV的特高压直流,大部分直流落点在华东电网和珠三角地区。目前南方电网已建成“8 交 8 直”交直流混合运行网络,其中直流通道输送功率占比约为 70%~80%。同样,在华东电网也已形成多馈入交直流混合运行电网[5]。多馈入直流输电对整个电网的稳定运行提出了极大的挑战。因此研究多馈入直流输电下的交直流混合电网特性,显得尤为重要。目前交直流侧谐波问题以及换相失败问题是阻碍LCC-HVDC发展的两个主要原因。在交流系统正常运行时,已有大量的文献准确分析交直流侧的特征次、非特征次谐波;然而,当交流发生故障,锁相同步环节失去锁相能力,被强制为故障前的同步相位[6]。此时的触发控制无法根据交流系统的实际情况给出脉冲信号,交直流侧的谐波将变得复杂。已有的谐波分析中,并未考虑锁相同步环节的影响,不能准确、清晰的阐释交流系统故障时的谐波含量与来源。因此,有必要在获取准确同步相位的基础上,建立换流器模型,分析交直流侧的谐波,以便降低故障对直流输电系统的影响。
........
1.2 国内外研究现状
对交直流侧谐波的清晰阐释,关键在于获取准确的同步参考相位、建立准确的换流器数学模型。本论文的研究从锁相环技术、高压直流输电换流器建模这两部分出发。以下分别对它们的国内外研究现状进行总结与分析。
1.2.1 锁相环技术
常规高压直流输电的控制系统对换流器的控制调节作用最终通过触发相位控制来实现。一般有两种触发相位控制,即分相触发控制和等间隔触发控制。由于等间隔触发控制在交流系统故障、畸变时,能够抑制谐波振荡、低次谐波的产生,现代直流输电一般采用此触发方式[1]。实现等间隔触发控制需要获取与交流系统同步的参考相位,现代直流输电系统通过锁相环技术来实现。因此,研究、采用性能优良的锁相环技术,对于准确分析直流系统的谐波特性、实现精确控制,意义重大,是后续研究的一个基础。文献[6; 10]介绍了实际直流工程中的一种锁相环,基本结构如图 1-1 所示。该锁相环利用复数FIR数字滤波器提取基波正序电压,消除负序电压与谐波对锁相环的影响。然而,交流系统故障时,由于滤波器本身的延时,锁相环无法快速提供稳定、准确的同步参考相位,降低了锁相环的动态性能,因此直流系统被强制按照故障前的同步相位触发[6],失去了对交流系统的跟踪能力。而且复数FIR数字滤波器的实现与分析较复杂。
........
第二章 锁相环基本原理及分析
在电网电压不平衡、畸变等条件下,由于受到负序分量、谐波等影响,SRF-PLL的输入信号中将出现波动分量,不再能够准确跟踪电网的电压相位。常用的办法为通过提取电网电压中的基波正序分量,作为SRF-PLL的输入信号。因此,目前大部分研究改善三相锁相环性能的方法,主要集中在如何提取基波正序电压。本章首先介绍SRF-PLL锁相环的基本原理以及不平衡、畸变等条件下的锁相误差分析,再介绍DDSRF-PLL与CDSC-PLL两种锁相方式,分析它们在低次谐波存在时的锁相误差,最后在PSCAD中对三种锁相方式的性能进行仿真分析与验证。
2.1 SRF-PLL原理及误差分析
在三相电压平衡的情况下,锁相环响应速度很快,能够准确锁定电网的相位,并能够测量电网的频率。但是,当三相电压不平衡,或者产生畸变时,SRF-PLL将不再能够准确、快速锁定同步相位,测量到的频率会产生波动。
.........
2.2 DDSRF-PLL原理及误差分析
2.2.1 DDSRF-PLL基本原理
为解决三相电压不平衡时SRF-PLL无法准确、快速锁定相位的问题,Pedro Rodríguez等学者提出解耦双同步旋转坐标锁相环(Decoupled Double Synchronous Reference FramePhase Locked Loop, DDSRF-PLL)[14]。当三相电压不平衡,且仅考虑基波电压时,式(2-6)可简化为:在上一节式(2-7)中可知,变换到正方向(正序电压)旋转的dq坐标时,正序电压频率将会减去 1,而负序电压频率则会加上 1。因此,可以想到,若是dq坐标分别按照正方向、负方向旋转,则基波正序电压将会在正方向dq坐标系中变为直流量,而在负方向dq坐标系中变成 2 倍频交流量;同样,负序电压在负方向dq坐标系下变为直流,而在正方向dq坐标系成为 2 倍频交流量。这一特点为解耦提取正负序电压提供了基础。通过上面工作原理的分析,电压中仅有基波正负序电压时,DDSRF-PLL的解耦运算能够快速地将正序、负序电压分离,实现对基波正序电压相位的准确跟踪,这一点比SRF-PLL有了改进。然而,电网电压不可避免地含有谐波。特别是在高压直流输电交流系统发生故障时,换流器的整流/逆变过程,将产生非特征次谐波,其中低次谐波对系统电压波形影响极大。因此,有必要研究分析DDSRF-PLL对低次谐波的抵抗能力。
........
第三章 锁相环的改进与电压的计算.......22
3.1 环外解耦多旋转同步坐标锁相环.......22
3.1.1 DMSRF-PLL-Impr基本原理与改进....22
3.1.2 DMSRF-PLL-Impr下谐波电压的计算..........25
3.2 CDSC+解耦运算锁相环.............25
3.2.1 CDSC-PLL-Impr基本原理.........26
3.2.2 CDSC-PLL-Impr下谐波电压计算.......28
3.3 仿真验证........29
3.4 小结......37
第四章 高压直流换流器开关函数建模与谐波计算.............38
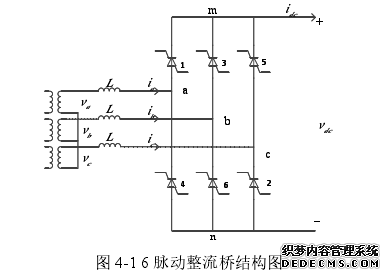
4.1 六脉动整流桥开关函数模型......38
4.3 换流器直流侧等值电路....44
4.4 开关函数模型仿真验证与分析............45
4.5 直流侧谐波计算......50
4.6 小结......54
第四章 高压直流换流器开关函数建模与谐波计算
换流器是高压直流输电系统中的核心设备,准确建立换流器的模型,对研究高压直流输电谐波、动态性能具有重要的意义。国内外对换流器的模型展开了大量的研究,主要的模型有电磁暂态模型、准稳态模型、开关函数模型等。其中,开关函数模型能够揭示谐波产生机理、物理概念清晰、计算简单等优点而得到广泛的应用。然而,现有开关函数模型主要适用于交流系统对称运行的工况,但当交流系统发生不对称故障时,现有开关函数模型则不能准确地模拟换流器的工作状况,需要进行修正本章针对现有开关函数模型的不足,提出一种基于正序电压锁相环,且同时适用于正常运行和不对称故障工况下的开关函数模型。该模型通过正序锁相环提供稳定、准确的同步参考相位,并在考虑换流器直流侧谐波阻抗的前提下,准确计算出不对称故障工况下阀电压过零点、换相角以及有效触发角。最后,在CIGRE Benchmark模型中设置不对称故障,仿真验证了该模型的准确性,并给出了模型的适用范围。以建立的开关函数模型为基础,将直流电压表达式展开,详细分析交直流侧的谐波关系,重点给出直流分量、2 次谐波幅值的计算式。在此基础上,提出用不对称触发角抑制直流侧谐波的方法,因此本章的开关函数模型将使用CDSC-PLL-Impr来提供基波正序电压同步参考相位。同时,由于整流桥与逆变桥结构相同,只是触发角所在象限不同,因此,本章以整流桥为例建立开关函数模型。#p#分页标题#e#

............
总结
随着直流通道输送功率占比逐渐提高,高压直流输电在我国现代电网中的重要地位日益凸显。针对交流系统故障时,高压直流输电锁相环无法准确锁定相位、交直流侧谐波相互影响等问题,本文提出了锁相环的改进方法,在此基础上建立了准确的换流器开关函数模型,并进行了仿真验证。主要内容总结为:
(1) 详细分析SRF-PLL、DDSRF-PLL及CDSC-PLL三种锁相环的基本原理与锁相误差。SRF-PLL的小信号模型为二阶系统,在三相电压对称的情况下,能够快速、准确地锁定电压相位;一旦电压不对称、畸变,SRF-PLL就无法提供稳定、准确的相位,本文对此进行了分析,并量化SRF-PLL的相位误差。鉴于SRF-PLL本身的缺陷,文中进一步介绍了DDSRF-PLL以及CDSC-PLL的基本原理。然而,当高压直流输电交流系统故障存在含量较高低次谐波的情况下,这两种锁相环仍然无法满足触发控制系统的要求。文中分析了低次谐波对这两种锁相环的影响,并在PSCAD中设置各种工况,仿真验证对这三种锁相环的分析。
(2) 高压直流输电交流系统发生故障时,主要的电压成分为±1、±2、±3 次电压。±2 次电压主要在暂态过程中存在。针对此特点,引入了解耦多旋转坐标系,采用解耦运算的方法提取基波正序电压。但是,由于解耦单元依赖于锁相环反馈的同步相位,两者之间相互影响,造成动态过程中的振荡。由于一般情况下,电网频率稳定,变化非常缓慢。根据这一特点,本文提出将解耦单元移出锁相环 外 , 解 耦 运 算 的 结 果 经 PARK 逆 变 换 后 作 为 锁 相 环 输 入 , 形 成DMSRF-PLL-Impr。针对级联信号延迟消除法CDSC需要 0.5 个周期滤除+2 次谐波的缺点,文中提出将CDSC输出的结果进行锁相环外解耦运算提取+1 次电压,形成CDSC-PLL-Impr。同时,在改进后的锁相环基础上,计算出±1、±2、±3 次电压。最后在PSCAD中设置各种电压工况,验证了改进后的两种锁相环在性能上都得到较大的提高。而CDSC-PLL-Impr的性能比DMSRF-PLL-Impr又略胜一筹。
(3) 换流器是高压直流输电系统中的核心设备,实现整流/逆变的功能。然而,换流器又是一个谐波源,在交流系统不对称故障时,换流器的交直流侧之间的谐波关系变得复杂。针对现有开关函数模型在不对称故障时准确性差、需要修正模型等缺点,本文提出基于实际电压过零点的开关函数模型。利用CDSC-PLL-Impr能够提供稳定、准确同步参考相位的优点,使用交流电压的正负序分量实时计算换相电压过零点,进而计算出各阀的换相角、有效触发角,将此三个要素考虑,建立各相的开关函数模型,准确反映了阀的导通、关断情况。文中提出的电压过零点、换相角、有效触发角计算式,同时适用于正常和不对称故障工况,建立的开关函数模型不需修正。最后在CIGRE Benchmark标准直流模型中验证了开关函数模型以及相关计算式的正确性。并且通过仿真,指出了模型的适用范围。
(4) 将三相电压用对称分量法表示,开关函数与相电压的乘积之和为直流电压,对直流电压表达式进行化简后,即可清晰反映交流侧的h次谐波电压在直流侧以n-h、n+h两种谐波形式存在。文中给出了直流侧谐波的简便的计算方法,特别讨论了直流分量和 2 次谐波分量。直流侧 2 次谐波表达式显示,在交流系统故障确定的情况下,能够通过调整三相触发角来实现抑制 2 次谐波。对此,文中经优化得到一组三相触发角,在PSCAD中搭建模型,验证了方法的可行性。
..........
参考文献(略)

